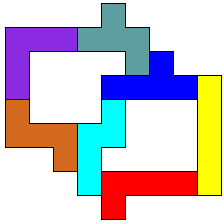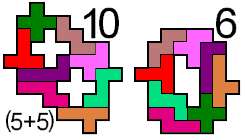Omsluiting met een symmetrie-middelpunt

Van Aad Thoen kregen we nog een uitdaging:
Maak een zo groot mogelijke symmetrische (zowel binnen als buiten) omsluiting met een symmetrie-middelpunt

We kregen een oplossing van 44 met 10 pentomino's.

Met een oneven aantal pentomino's in een puntsymmetrie moet één pentomino het centrale veld
van puntsymmetrie bezetten wat tweedeling als gevolg heeft

George Sicherman: "Here are all the two-hole 3-pentomino solutions"

Met 4 pentomino's

(OM en HP)

(AW)

Met 5 pentomino's (AT en AW)

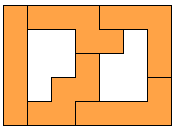
Deze is wel heel mooi omdat de ingesloten ruimten ook een pentomino is.

Met 6 pentomino's
Aad van de Weteringvond deze met de hand.


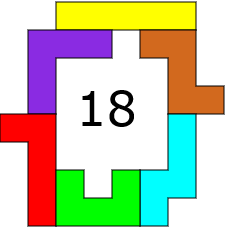
Met 7 pentomino's

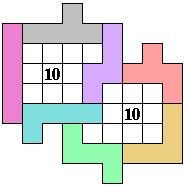
(OM)

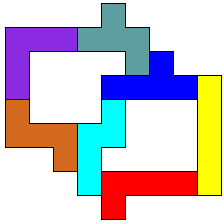
(AW)

Aad Thoen stuurde nog twee andere oplossingen.


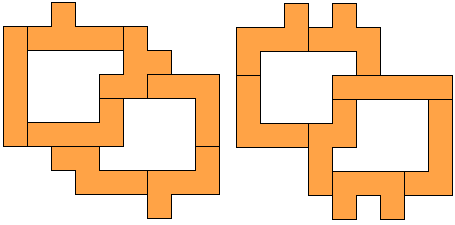
Met oneven pentomino's in puntsymmetrie is dat dan congruentie niet nodig is.

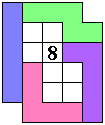
Met 8 pentomino's
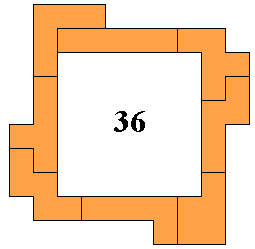
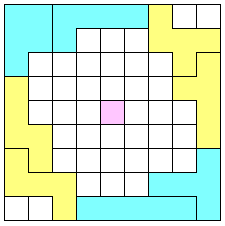
Aad Thoen : "Mijn methode is gebaseerd op congruenties, de voorbeelden spreken voor zich. In de 6x6-omsluiting zult u de congruenties wel kunnen herkennen. In de 37-omsluiting is het centrale veld van symmetrie met een kleurtje aangegeven."

Deze laatste kan heel makkelijk naar 2 meer.

 

Aad Thoen vond er nog eentje bij

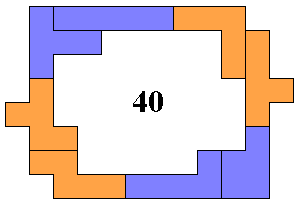en nog eentje...

Deze laatste zal wel het record zijn want we kregen dezelfde oplossing van Helmut Postl.

Met 9 pentomino's

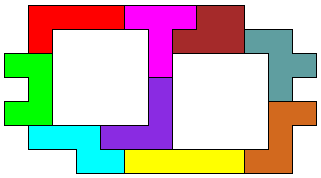
32 (AW)

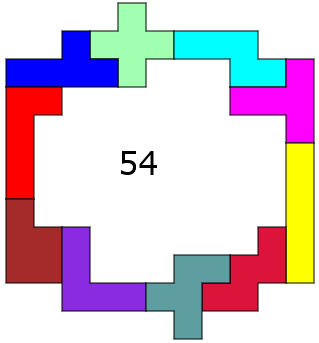
 Met 10 pentomino's
Aad van de Wetering:"Met de hand gevonden. Je legt een stel pentomino’s tegen elkaar aan, en daarna een ander stel er precies bovenop. Als het past, de bovenste eraf halen, 180 graden draaien en tegen de onderste aanschuiven. Zo simpel is het…"

Maar Helmut doet er eentje bij


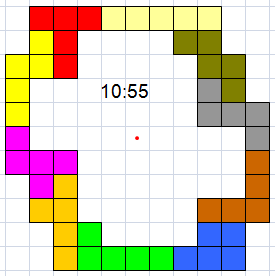
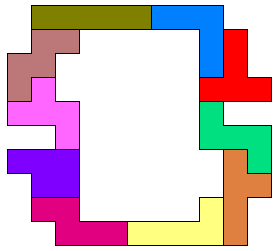
Met 11 pentomino's

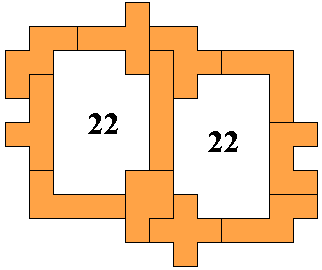
44(AT)


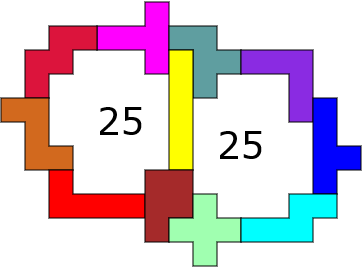
Aad van de Wetering: " Twee pentomino’s verwisselen (niet YU maar YZ) levert een verbetering op."
"Dat dubbelen werkt fantastisch!"



Met 12 pentomino's
Aad (Thoen) zond er ook eentje met een set:

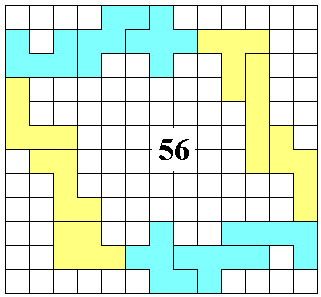
Dit is een oplossing van onze geliefde Pieter Torbijn (†)

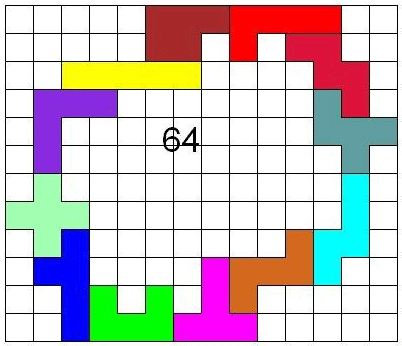
Aad van de Wetering brak dit record

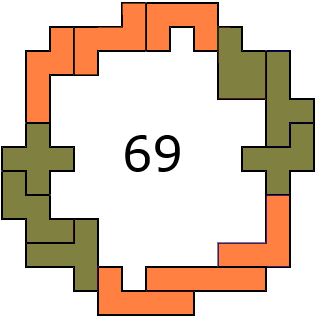
"... en allemaal handwerk, op het tekenen na. Het zijn twee paartjes van drie pentomino's: LIV en UZN, FYP en XWT. Als je er vier 15-omino's van maakt kun je daar leuk mee combineren"


Helmut Postl doet echter nog beter


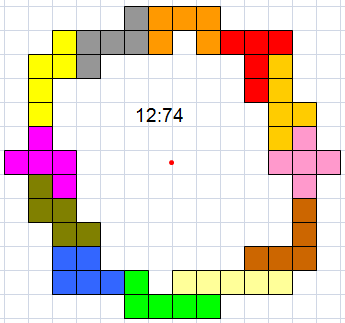
Van Aad van de Wetering kregen we een heel leuke  uitbreiding: een omheining met driedubbel paartjes.


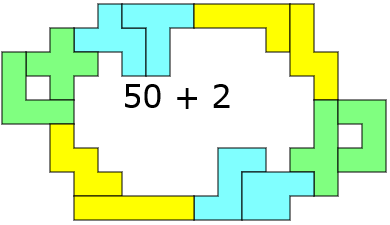
We zochten er eentje met een omheining in één geheel

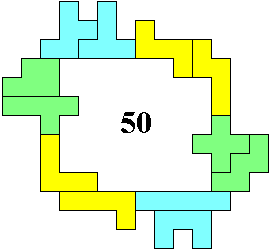
Om deze te vinden gebruikten we de oplossingen van Helmut Postl voor het potpourri-probleem 21

Edo Timmermans stuurde ter gelegenheid van onze wedstrijd 51 heel wat uitbreidingen met symmetrie-middelpunt.
Met alle pentomino's.

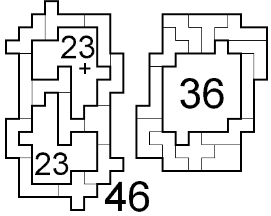
Hij stuurde ook omheiningen met 8 pentomino's die de ontvouwing zijn van een leeg doosje.

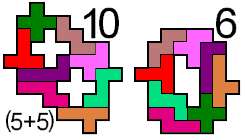
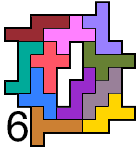
Edo zocht ook omheiningen met de hexomino's die de ontvouwing zijn van een kubus.