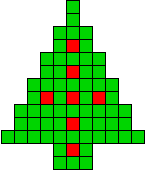
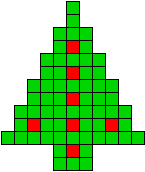
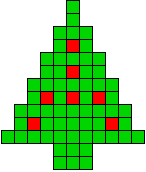
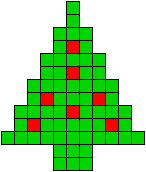
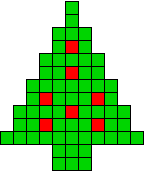
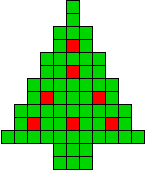
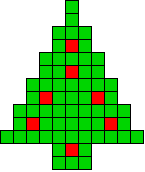
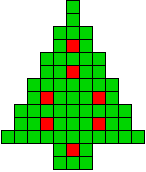
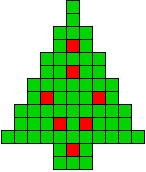
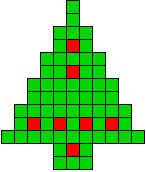
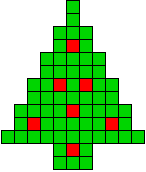
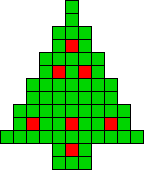
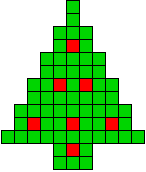
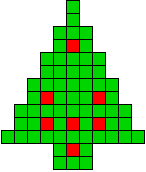
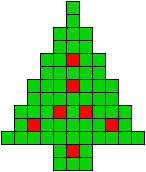
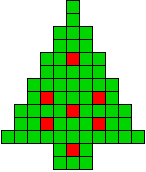
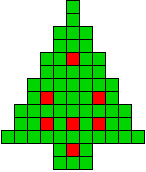
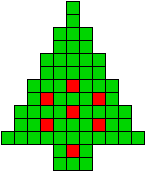
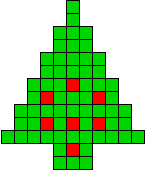
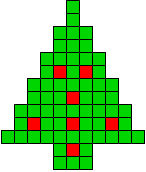
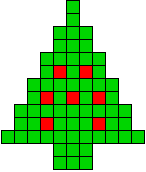
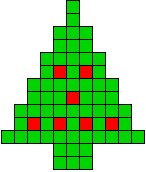
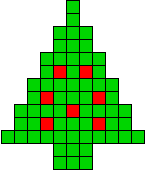
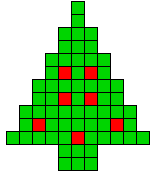
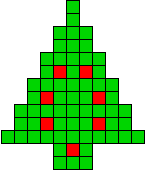
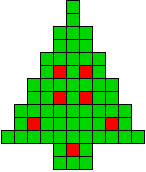
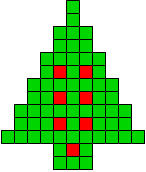
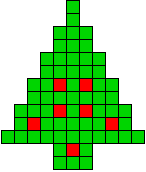
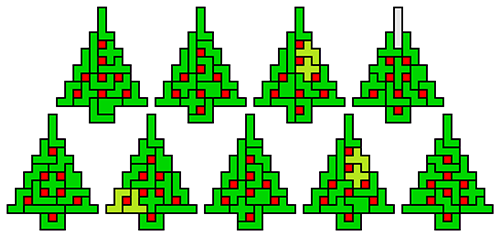
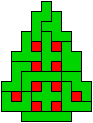
We kregen van Edo Timmermans de volgende kerstboompjes.
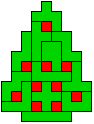
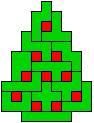
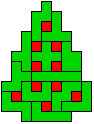
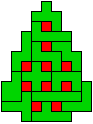
We gingen op zoek naar dezelfde vorm met de 7 kerstballen zodanig geplaatst dat ze elkaar niet raken (ook niet in de hoekpunten) en dat het geheel een symmetrieas heeft.
De kerstballen mogen ook de rand van de boom niet raken, ook niet in de hoekpunten.
We vonden er 27. Kan je er nog vinden? Laat het ons weten.
Edo vond er eentje bij! Dank. Er zijn er nu 28
Klik op de boom voor de oplossingen.
|
|
|
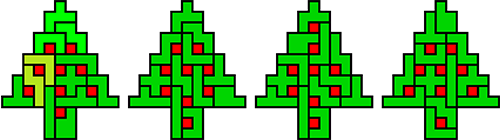
Edo: "Ik heb gezocht naar bomen met 8, 9 en 10 kerstballen. In bomen met verschillende kleuren groen is dat extra groen er om een symmetrisch gedeelte aan te geven. Bomen in egaal groen hebben 1 oplossing. De boom met 8 ballen en de T en Z pentomino's anders gekleurd heeft 4 oplossingen."
|
|
|
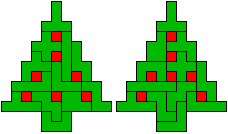
Edo: "Voor bomen met 10
kerstballen heb ik geen oplossingen gevonden met een volledige
pentomino-set, maar wel met een symmetrie-as zoals in het
oorspronkelijke
probleem"
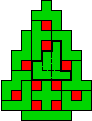
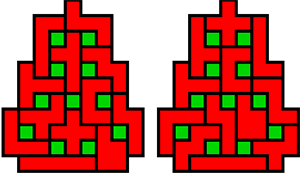
Edo: "Ook nog even naar een boom met
11 kerstballen gezocht, uiteindelijk heb ik er wel een gevonden, maar omdat
die vorm meer op een aardbei met 11 pitjes lijkt dan op een kerstboom met 11
kerstballen heb ik de kleuren omgewisseld. Het is een bijzondere aardbei,
omdat hij precies 2 oplossingen heeft waarbij 11 pentomino's op zijn minst
een klein beetje van positie zijn verandert. Alleen de T heeft dezelfde
positie in beide oplossingen."
We zochten een vorm waar dat wel kon.


![]()