Kerstboom en symmetrie
Aan het kerstboompje (dat bestaat uit 61 groene vierkanten) hangen 6 rode kerstballen (rode vierkantjes).

Verhang de kerstballen zodat ze symmetrisch hangen.

De rode vierkanten mogen elkaar niet raken, ook niet in de hoekpunten.

Ze mogen ook niet aan de buitenrand van de kerstboom hangen.

De grijze vierkanten mogen niet rood worden

Er zijn 163 mogelijkheden om zes ballen symmetrisch in een kerstboom te hangen, waarbij deze ballen niet elkaar noch de rand mogen raken.
Wil je de oplossing zien?

Nu de kerstballen symmetrisch hangen proberen we de rest van de boom te vullen met pentomino's (we hebben er 11 nodig) maar zodat de oplossing een symmetrieas heeft.
Congruente pentomino's mogen elkaar niet raken (wel in de hoekpunten)

De blauwe vakjes moeten zeker bedekt worden met een of ander (geel) vierkantje van I-, T-,U- of X-pentomino.

 0 kerstballen op de symmetrieas.
Hieronder zie je de symmetrieassen die je kan leggen zonder kerstballen op de symmetrieas. Het getal geeft aan hoeveel verschillende oplossen erbij behoren.

Hieronder zie je nog symmetrieassen maar die kunnen geen oplossing geven want je kan geen 3 kerstballen hangen (die aan de gestelde voorwaarde voldoen) in het linkse groene deel.

Ook onderstaande symmetrieas kan niet want bij de enige mogelijke plaatsing van 3 kerstballen raken de T-pentomino's elkaar.

Als je op de kerstboompjes drukt zie je de verschillende oplossingen.


6 oplossingen


7 oplossingen


7 oplossingen


18 oplossingen


22 oplossingen


19 oplossingen


13 oplossingen


17 oplossingen


23 oplossingen


15 oplossingen


17 oplossingen


11 oplossingen

2 kerstballen op de symmetrieas.

Als er een kerstbol hangt op plaats 1 of op plaats 2 is er geen invulling met pentomino's mogelijk.

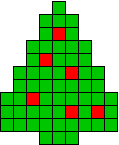
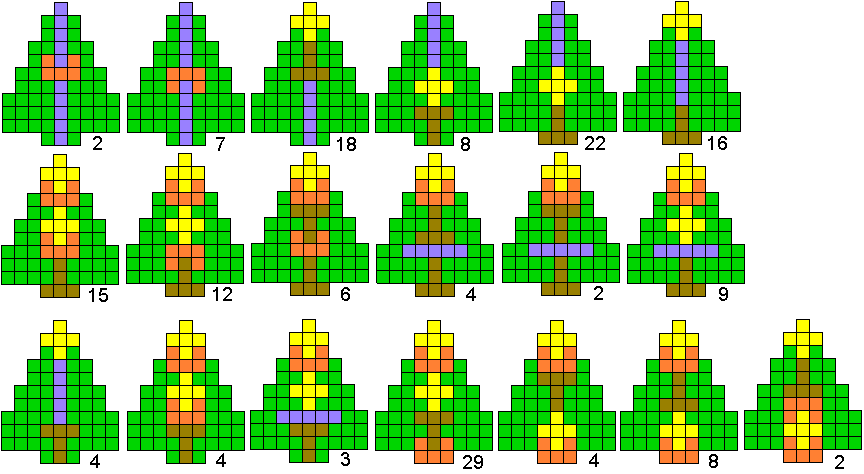
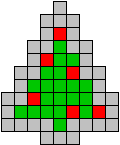
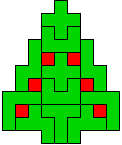
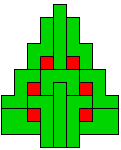
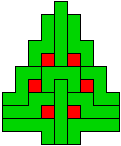
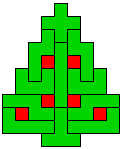
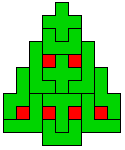
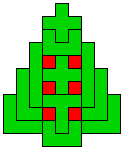
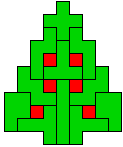
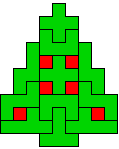
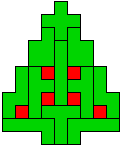
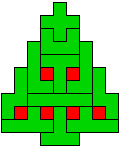
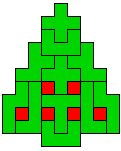
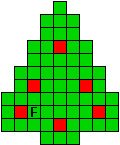
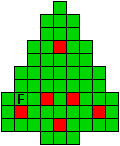
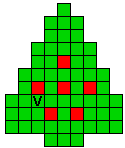
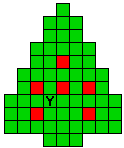
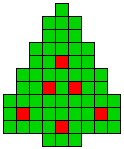
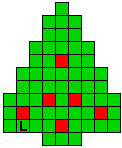
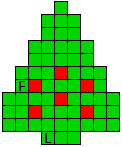
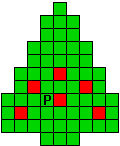
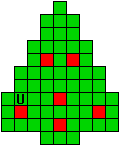
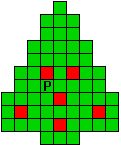
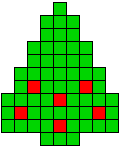
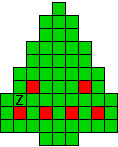
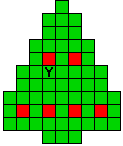
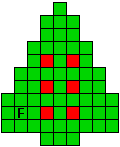
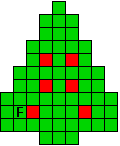
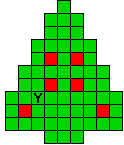
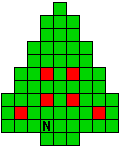
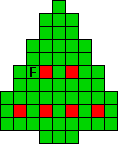
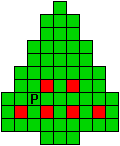
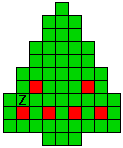
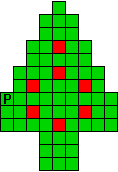
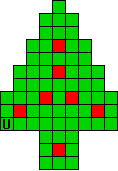
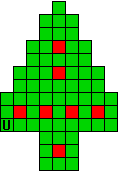
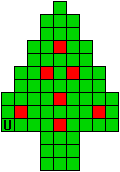
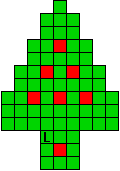
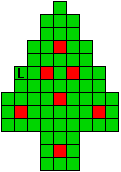
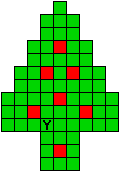
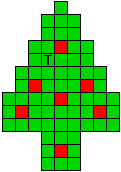
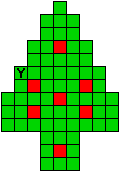
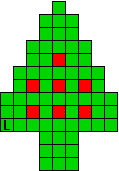
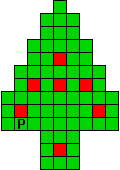
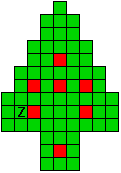
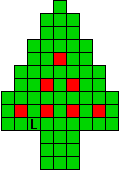
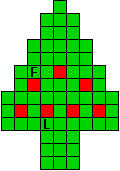
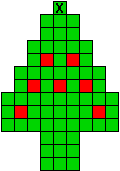
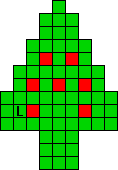
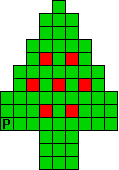
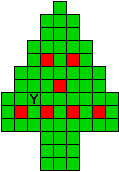
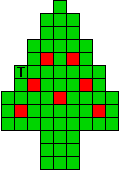
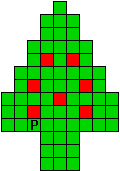
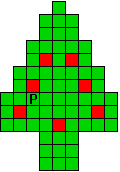
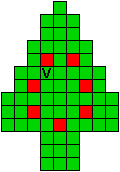
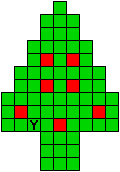
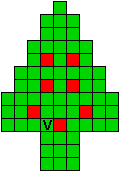
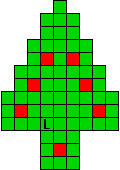
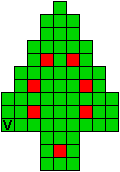
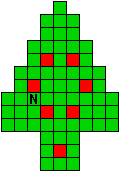
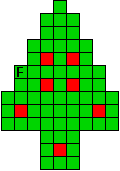
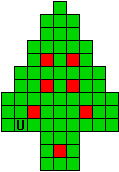
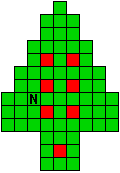
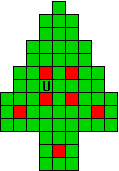
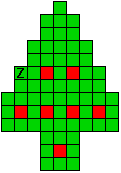
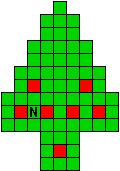
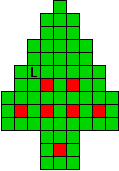
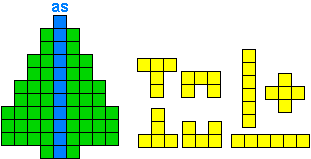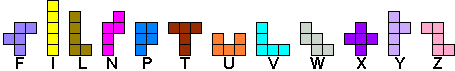Hieronder zijn alle mogelijkheden getekend die je kan opvullen met pentomino's zodat de oplossing een symmetrieas heeft.
Met dank aan Aad van de Wetering en zijn FlatPoly.
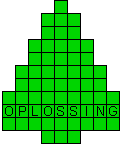
Als je op de kerstboompjes drukt zie je de oplossingen maar veel leuker is het van zelf te zoeken.


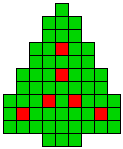
2 oplossingen


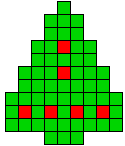
3 oplossingen


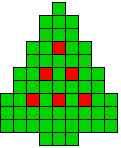
11 oplossingen


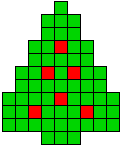
16 oplossingen


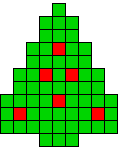
21 oplossingen


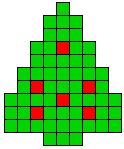
7 oplossingen


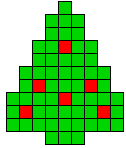
5 oplossingen


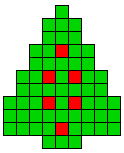
2 oplossingen


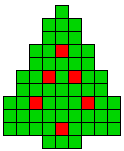
5 oplossingen


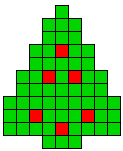
4 oplossingen


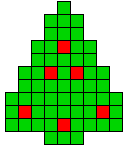
4 oplossingen


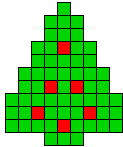
1 oplossing


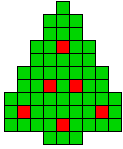
5 oplossingen


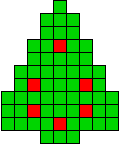
5 oplossingen


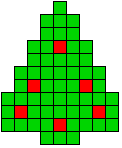
10 oplossingen


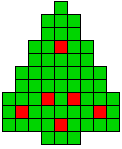
4 oplossingen


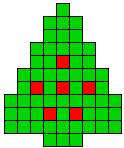
6 oplossingen


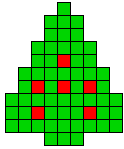
6 oplossingen


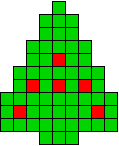
5 oplossingen


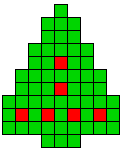
8 oplossingen


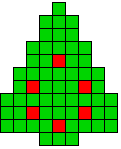
1 oplossing


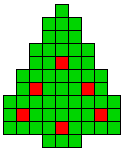
5 oplossingen


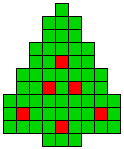
1 oplossing


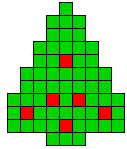
7 oplossingen


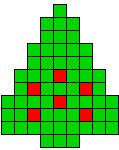
6 oplossingen


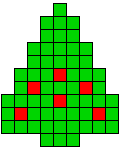
13 oplossingen


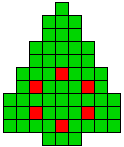
10 oplossingen


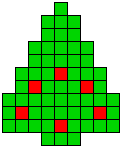
19 oplossingen


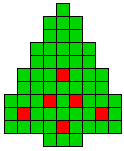
19 oplossingen


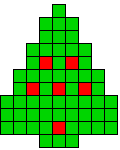
2 oplossingen


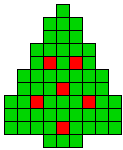
2 oplossingen


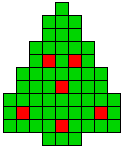
1 oplossing


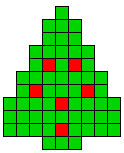
4 oplossingen


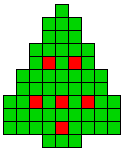
2 oplossingen


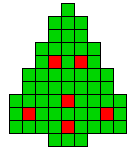
3 oplossingen


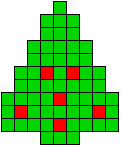
3 oplossingen


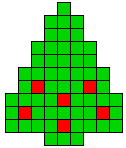
1 oplossing

Met 4 kerstballen op de as is er geen opvulling mogelijk.

Je kan een puzzel maken met elk van de vorige oplossingen

Lowie loste er op nieuwjaarsdag (2023) enkele op.

Je kan ook een pentoe maken. Dit wil zeggen dat de puzzel juist één oplossing heeft.
Hieronder staan nog eens de pentomino's met hun overeenkomende letters.

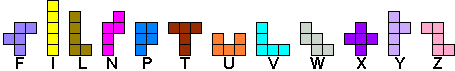
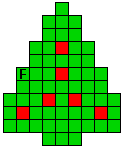
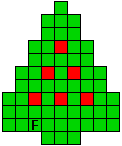
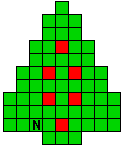
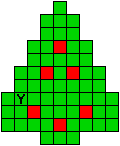
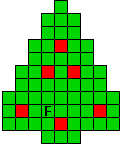
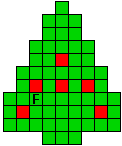
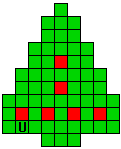
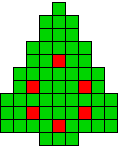
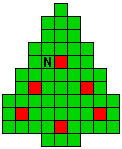
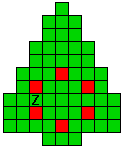
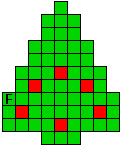
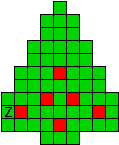
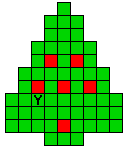
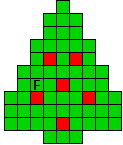
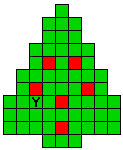
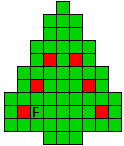
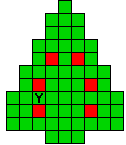
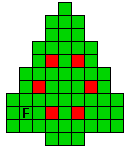
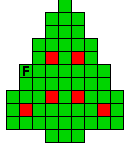
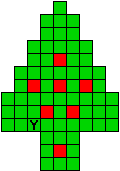
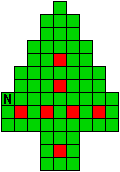
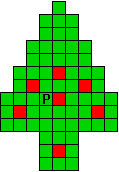
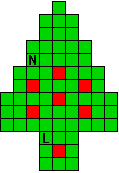
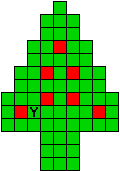
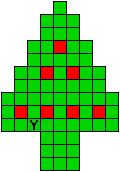
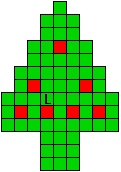
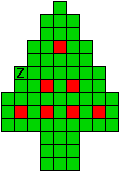
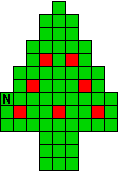
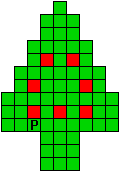
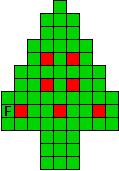
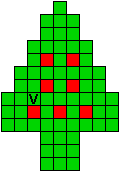
Verdeel de groene vakjes van de kerstboom in pentomino's zodat geen twee pentomino's met dezelfde vorm (ook niet gedraaid of gespiegeld) een zijde gemeen hebben. Een vierkantje met een letter in moet deel uit maken van de pentomino met dezelfde naam (zie hierboven). De oplossing moet een symmetrieas bezitten.

       

Wil je nog meer pentoes?
https://pentomino.classy.be/pentoesvoorblad.html

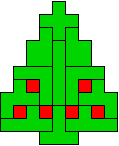
Edo Timmermans: "Als beloning voor al dat werk heb ik een paar kerstbomen met 12 pentomino's en 7 kerstballen gekweekt."

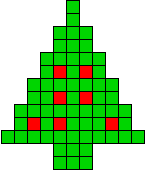
We vonden de vorm heel leuk om uit te werken maar dan met 7 ballen die symmetrisch hangen.
Hieronder zijn alle mogelijkheden getekend die je kan opvullen met pentomino's zodat de oplossing een symmetrieas heeft.
Met dank aan Aad van de Wetering en zijn FlatPoly.
Als je op de kerstboompjes drukt zie je de oplossingen maar veel leuker is het van zelf te zoeken.

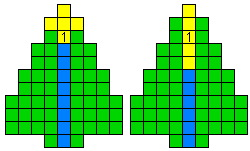
Op de symmetrieas hangen 5 ballen
Er is maar 1 mogelijkheid en die heeft juist één oplossing


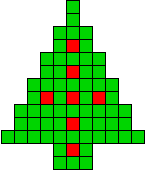
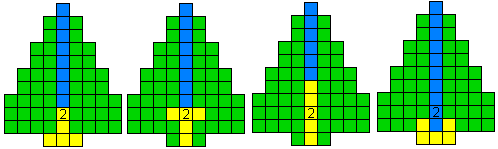
Op de symmetrieas hangen 3 ballen of 1 bal


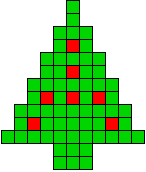
1 oplossing


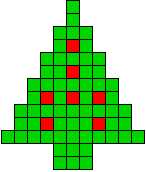
2 oplossingen


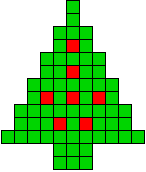
4 oplossingen


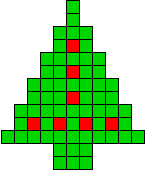
4 oplossingen


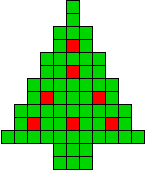
6 oplossingen


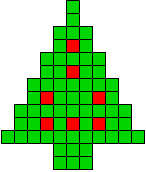
3 oplossingen


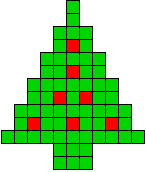
5 oplossingen


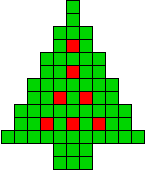
4 oplossingen


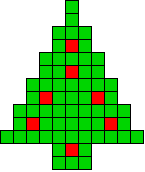
7 oplossingen


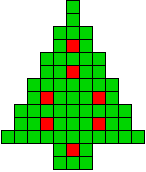
6 oplossingen


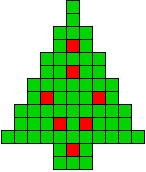
3 oplossingen


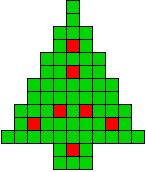
4 oplossingen


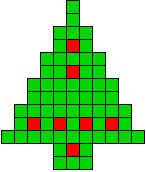
5 oplossingen


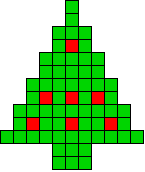
1 oplossing

 
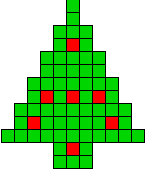
3 oplossingen


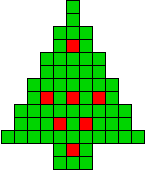
3 oplossingen


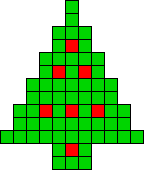
2 oplossingen


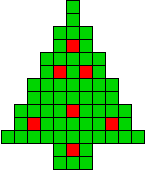
3 oplossingen


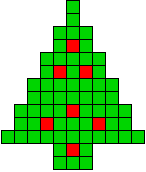
6 oplossingen


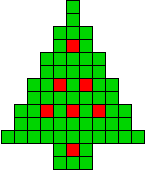
3 oplossingen

 
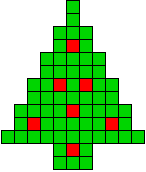
4 oplossingen


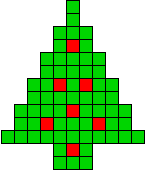
7 oplossingen


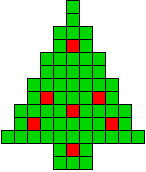
1 oplossing


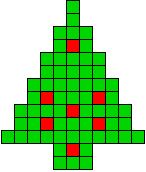
4 oplossingen


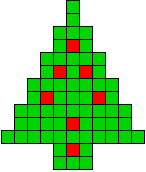
5 oplossingen


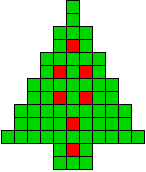
8 oplossingen


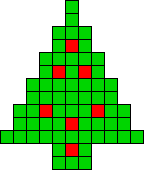
6 oplossingen


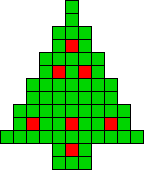
7 oplossingen


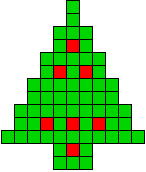
9 oplossingen


8 oplossingen


6 oplossingen


11 oplossingen


8 oplossingen


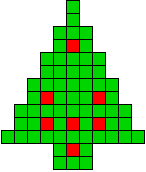
9 oplossingen


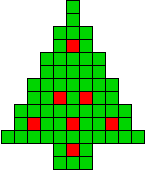
5 oplossingen


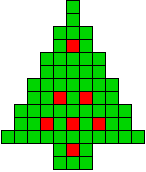
5 oplossingen


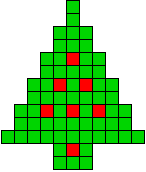
2 oplossingen


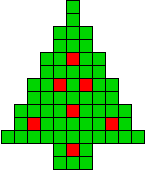
4 oplossingen


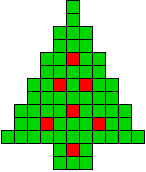
5 oplossingen


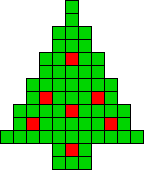
1 oplossing


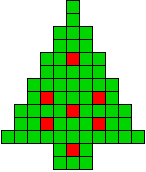
4 oplossingen


3 oplossingen


6 oplossingen


5 oplossingen


2 oplossingen


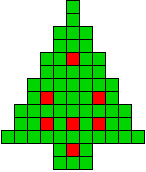
4 oplossingen


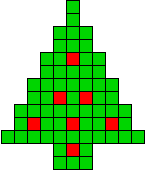
3 oplossingen


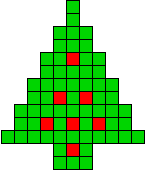
3 oplossingen


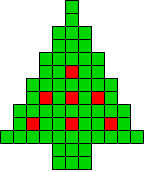
1 oplossing


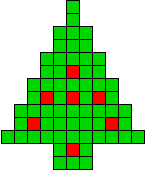
3 oplossingen


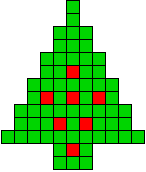
7 oplossingen


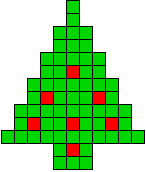
4 oplossingen


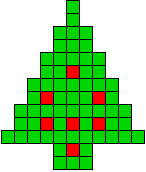
4 oplossingen


4 oplossingen


2 oplossingen


2 oplossingen


1 oplossing


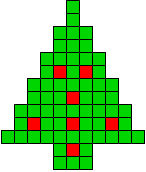
4 oplossingen


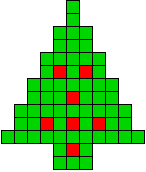
3 oplossingen


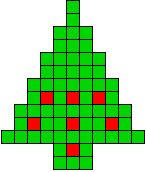
2 oplossingen


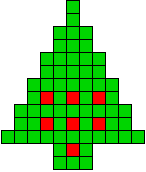
2 oplossingen


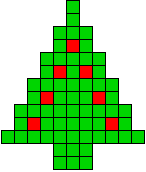
11 oplossingen


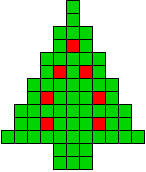
9 oplossingen


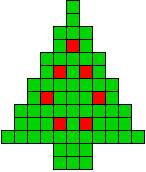
15 oplossingen


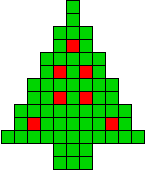
20 oplossingen


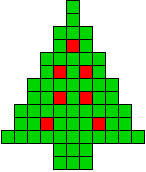
14 oplossingen


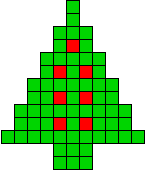
14 oplossingen


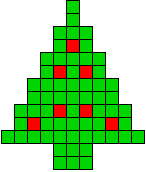
13 oplossingen


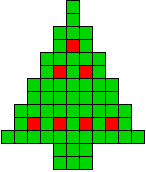
20 oplossingen


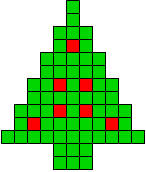
11 oplossingen


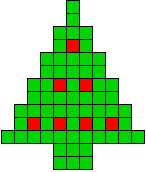
24 oplossingen


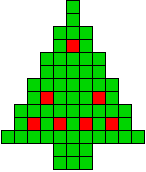
14 oplossingen


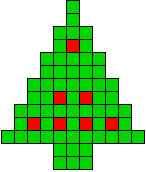
10 oplossingen


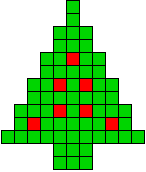
8 oplossingen


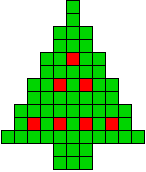
19 oplossingen


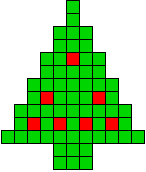
7 oplossingen


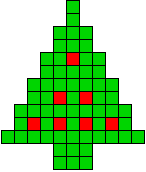
7 oplossingen


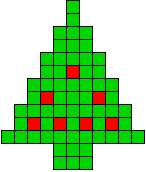
1 oplossing


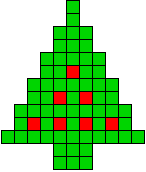
11 oplossingen


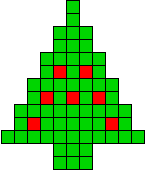
5 oplossingen


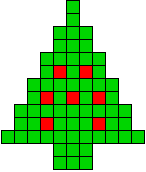
3 oplossingen


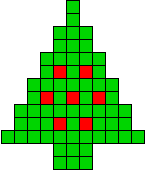
9 oplossingen


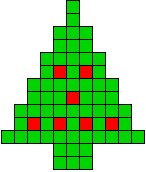
13 oplossingen


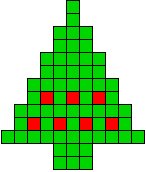
8 oplossingen


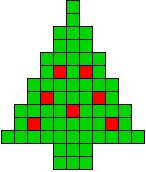
8 oplossingen


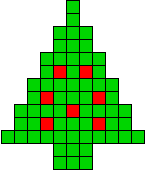
1 oplossing


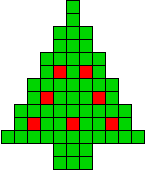
7 oplossingen


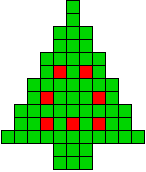
1 oplossing


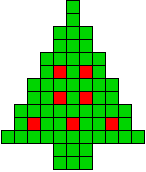
7 oplossingen


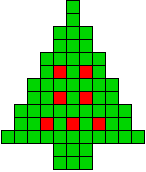
5 oplossingen


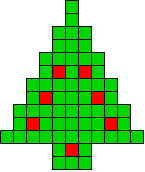
7 oplossingen


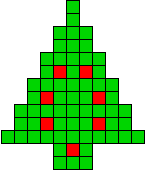
3 oplossingen


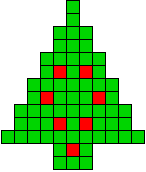
8 oplossingen


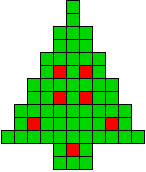
8 oplossingen


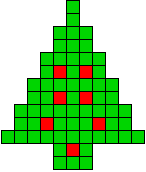
2 oplossingen


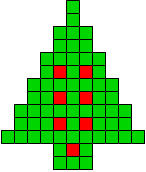
22 oplossingen


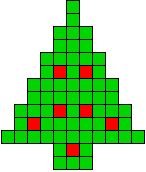
19 oplossingen


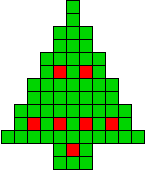
22 oplossingen


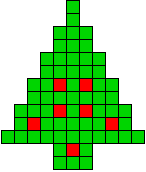
19 oplossingen


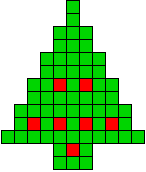
17 oplossingen


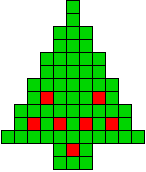
13 oplossingen


14 oplossingen


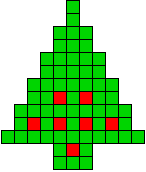
Edo stuurde ons de vorm met de ballen symmetrisch en opgevuld met een pentominoset. We vinden dit niet zo mooi als toepassing op symmetrie maar misschien vinden sommigen dit leuk als puzzel en daarom maakte we een afzonderlijke pagina.

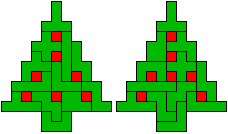
Edo stuurde nog een tweede kerstboompje deze maal gevuld met een pentominoset.

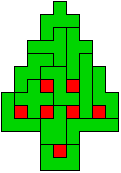
We willen echter dat de oplossing een symmetrieas heeft.
Met 5 ballen op de symmetrieas is er geen oplossing.
Op de symmetrieas hangen 3 ballen of 1 bal


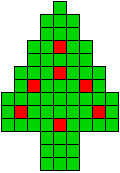
1 oplossing


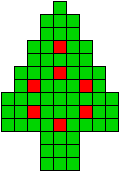
3 oplossingen


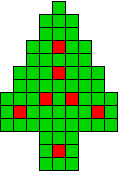
2 oplossingen


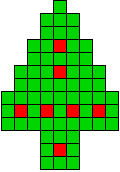
3 oplossingen


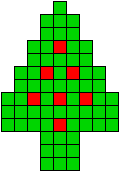
1 oplossing


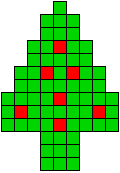
3 oplossingen


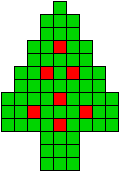
1 oplossing


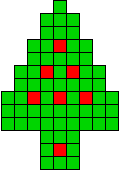
11 oplossingen


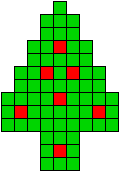
21 oplossingen


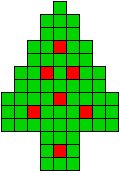
16 oplossingen


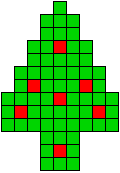
5 oplossingen


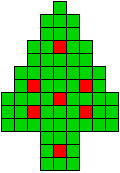
7 oplossingen


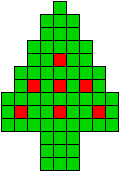
1 oplossing


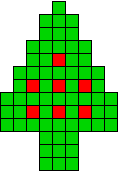
2 oplossingen

 
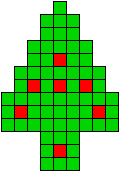
2 oplossingen


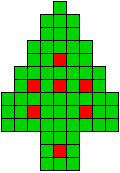
4 oplossingen


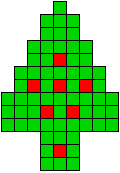
2 oplossingen


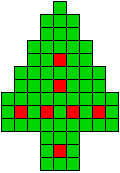
2 oplossingen


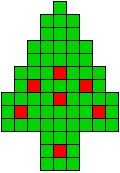
13 oplossingen


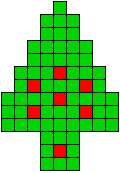
6 oplossingen

 
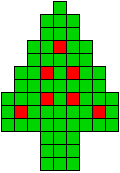
7 oplossingen


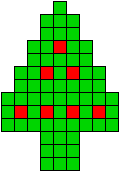
9 oplossingen


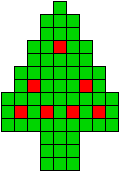
7 oplossingen


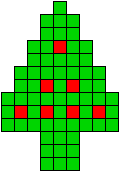
7 oplossingen


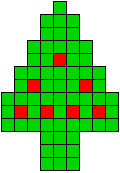
1 oplossing


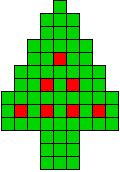
2 oplossingen


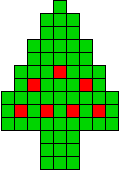
8 oplossingen


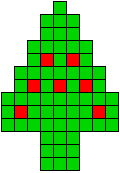
2 oplossingen


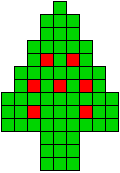
3 oplossingen


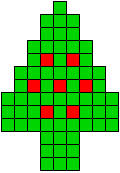
2 oplossingen


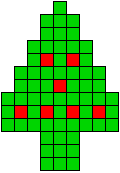
5 oplossingen


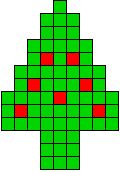
4 oplossingen


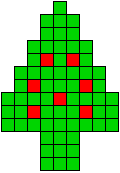
3 oplossingen


9 oplossingen


7 oplossingen


17 oplossingen


13 oplossingen


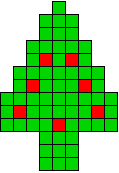
3 oplossingen


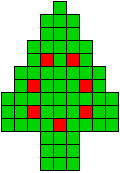
4 oplossingen


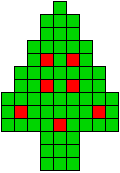
8 oplossingen


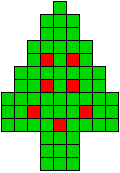
2 oplossingen


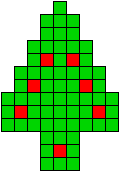
6 oplossingen


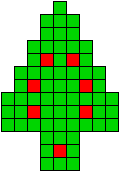
5 oplossingen


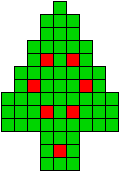
7 oplossingen


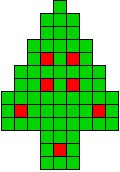
11 oplossingen


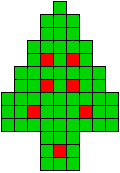
13 oplossingen


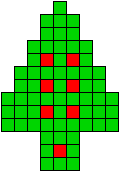
6 oplossingen


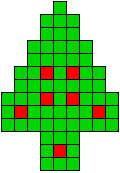
13 oplossingen


 


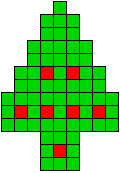
15 oplossingen


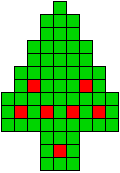
11 oplossingen


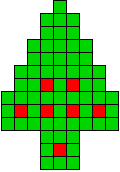
11 oplossingen


 


 

Ongelooflijk maar waar: we kregen van Nicole alle voorgaande pentoes opgelost, daarom volgt hier nog een serie.
Hieronder staan nog eens de pentomino's met hun overeenkomende letters.

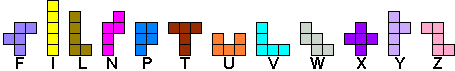
Verdeel de groene vakjes van de kerstboom in pentomino's zodat geen twee pentomino's met dezelfde vorm (ook niet gedraaid of gespiegeld) een zijde gemeen hebben. Een vierkantje met een letter in moet deel uit maken van de pentomino met dezelfde naam (zie hierboven). De oplossing moet een symmetrieas bezitten.







 


 















Nicole Verschuere kregen we ook van de tweede reeks alle oplossingen.
Renaat Steurbaut, Lieven Van Rijckeghem, Martine Oufflin, Eddy Moreau en Gert-Jan Stockman stuurde de oplossing van ons nieuwjaarskerstboompje.

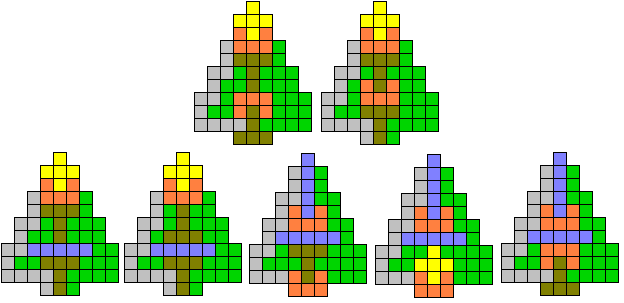
Edo ging maar door. Hij stuurde kerstboomjes met 8, 9 kerstballen die symmetrisch hangen en opgevuld met een pentoset.
We gingen op zoek naar symmetrische opvullingen.
Met 8 kerstballen


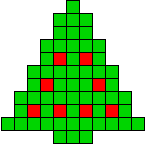
2 oplossingen


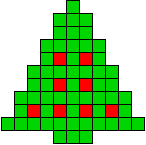
8 oplossingen


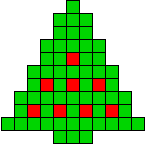
1 oplossing


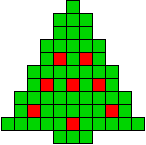
1 oplossing


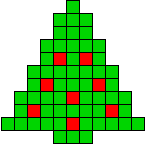
2 oplossingen

Met 9 kerstballen


1 oplossing


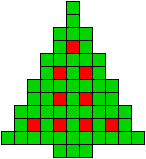
8 oplossingen


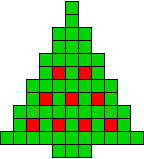
1 oplossing


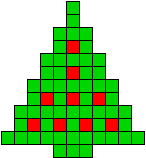
1 oplossing

Met 10 kerstballen


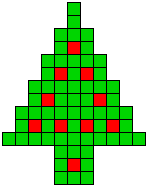
1 oplossing


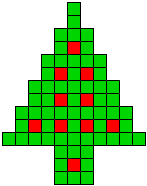
1 oplossing


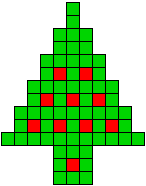
Van Edo. Dank


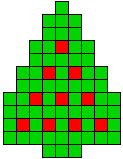
4 oplossingen


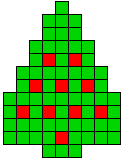
2 oplossingen


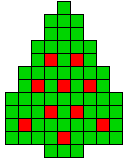
5 oplossingen


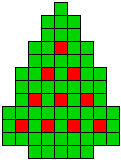
10 oplossingen


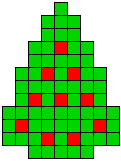
10 oplossingen


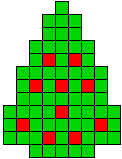
1 oplossing


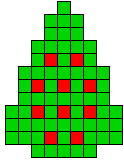
2 oplossingen


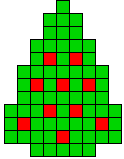
 32 oplossingen

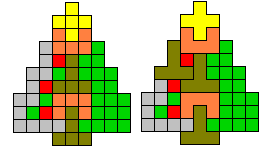
Edo: "Ook nog even naar een boom met 11 kerstballen gezocht, uiteindelijk heb ik er wel een gevonden, maar omdat die vorm meer op een aardbei met 11 pitjes lijkt dan op een kerstboom met 11 kerstballen heb ik de kleuren omgewisseld."


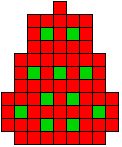
6 oplossingen


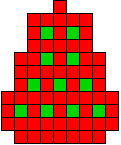
24 oplossingen


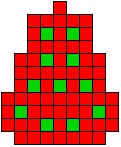
18 oplossingen


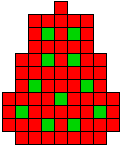
4 oplossingen

In onze workshop "Breinbrekers voor uitdagende wiskundelessen 3" op de dag van de wiskunde in Kortrijk op 25 november 2023 maakten we 2 soorten opgaven met pentominoeskerstboompjes.
De eerste was een gemeenschappelijke opgave.
Op de doos plakten we langs weerszijden hetzelfde kerstboompje. In de doos zaten 2 zakjes met 11 pentomino’s. We kozen twee verschillende opgaven. Met de 11 pentomino's kon men maar één oplossing leggen.
Tip: met de pentomino’s die op de symmetrieas moeten liggen beginnen.
De  tweede was één van onze keuzeopdrachten.
We kozen hiervoor de boompjes uit die maar juist één oplossing hebben.(zo zijn er 5: zie hierboven).
Bij deze opgave moet men zelf vinden welke pentomino's men moet gebruiken.
Wil je graag onze syllabus?
Stuur dan een mail naar OdetteDM@outlook.com


De leerlingen van Matthias Maes en zijn collega uit 't Saam (Campus Aloysius) in Diksmuide zochten reeds naar een oplossing van ons kerstboompjes.


Een afgesloten deel moet altijd een vijfvoud van vierkantjes zijn.

Tine Verplancke (Prizma Middenschool - Izegem) en haar leerlingen van 1B hielden een projectdag en hadden 4 opdrachten gebruikt (mits wat aanpassing en/of extra duiding) uit onze workshop.
 "De escape room was een erg succes bij de leerlingen én voor mij ook aangezien ze 60 minuten met wiskunde zijn bezig geweest"

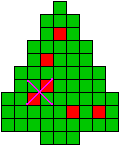
Op het kerstfeest 2023 werd er druk gezocht en gevonden.


De links naar meer pentominoes kan je vinden op het voorblad