Philo's probleem: 3 Pentomino's en symmetrie

Waarschijnlijk om de frustratie van wedstrijd 37 weg te werken kregen we van Philo het volgende probleem.
Philo's ploeteren kan je vinden bij records.
Verdeel de pentomino's in 4 groepen en maak van iedere groep een symmetrisch figuur, waarbij tussen minimaal twee pentomino's een symmetrie-as bestaat.
Philo vond 95 oplossingen voor zijn symmetrie-opgave.
Philo had een opmerking over onze site:"Je vermeldt een opgave op je website, maar geeft meteen een link naar de oplossingen.
Ik wil me - uiteraard - niet met je didactiek bemoeien, maar, gezien de creativiteit van je leerlingen, zou ik de vraag lanceren en laat ze maar met oplossingen komen. Daardoor ontstaat er m.i. voor iedereen een stimulans om meer/andere oplossingen te vinden."
Toch zijn we van plan van op onze eigen manier door te gaan.
Philo gaf een voorbeeld.

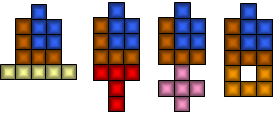
Elke vorm bestaande uit 3 pento's heeft hier een verticale symmetrie-as en de deelgroep PV heeft dat ook.
Oorspronkelijk begrepen we de bedoeling niet echt goed en gingen bij Aad te rade. Hij maakte voor ons de volgende tekening.

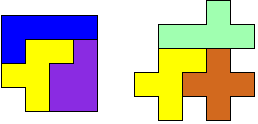
FLP heeft een symmetrie-as en FP ook.
FXY heeft een symmetrie-as, FX en FY ook.
Nu we het begrepen gingen we op zoek naar een oplossing.

Philo had een lijst toegevoegd die uitging van ons overzicht van alle vormen bestaande uit 2 pentomino's die een symmetrie-as hebben.
Aad merkte op dat FLP er niet tussen stond.
We vonden ook FX+Y en NZ+P niet.
Reden(denken we): een ander soort symmetrie-as. Voorbeeld:FX heeft een horizontale symmetrie-as en FXY een schuine.
Nadat Aad van de Wetering de volgende mail ontvingen gingen we verder zoeken:"Om alle symmetrische pentotrio’s te vinden heb ik Poly3D wat aangepast. Na zo’n 24 uur had ik alle 855 oplossingen gevonden. Programmeer- en denkfouten voorbehouden! Ze staan op http://home.wxs.nl/~avdw3b/pentosymm3.html"
We zochten de  symmetrisch figuren waarbij tussen minimaal twee pentomino's een symmetrie-as bestaat.(Hopelijk hebben we ze allemaal)

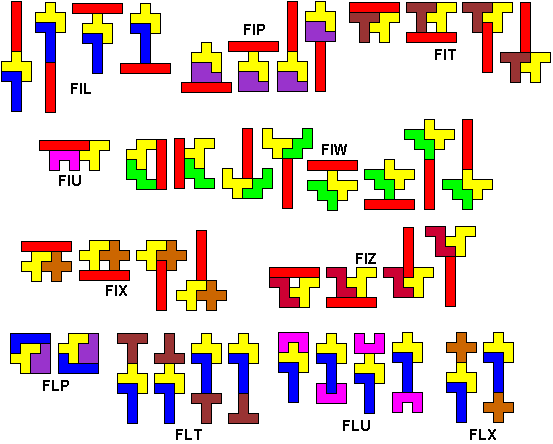
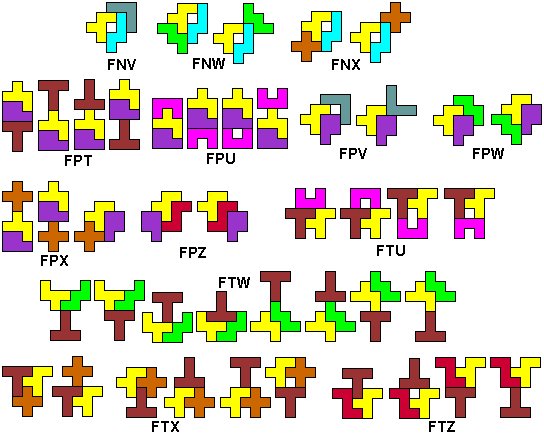
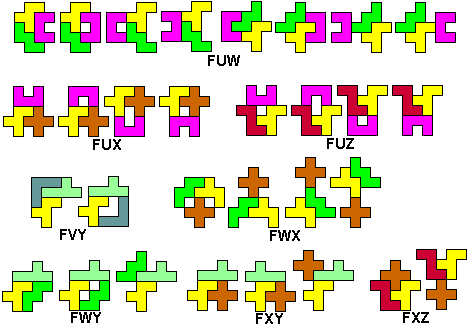
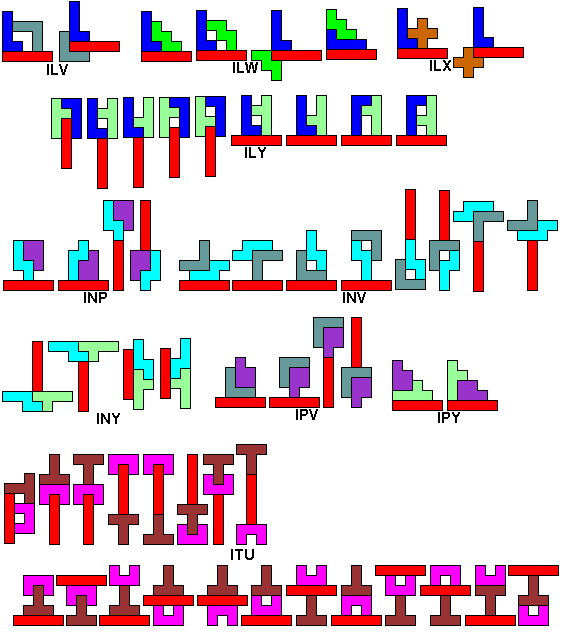
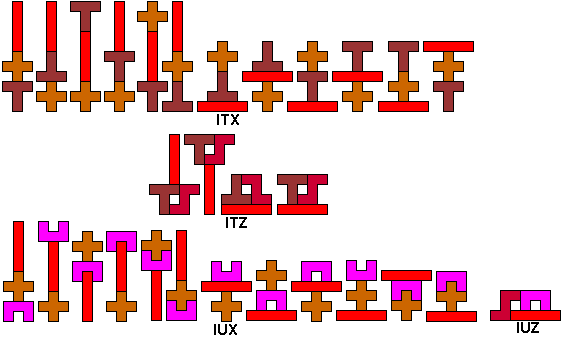
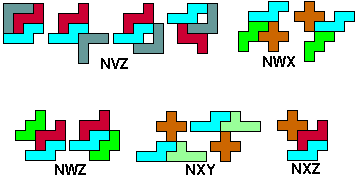
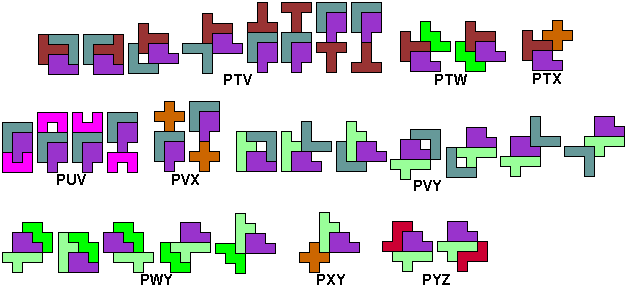
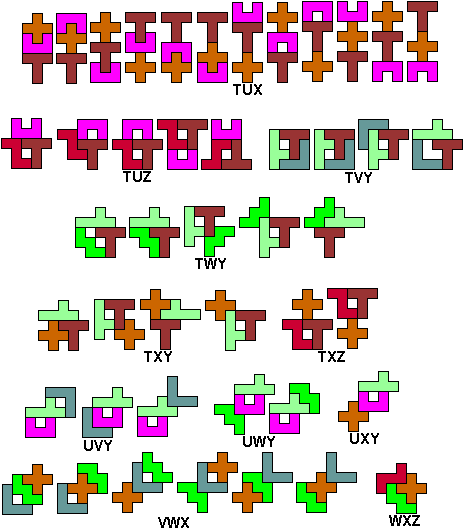
Commentaar en zeker andere oplossingen zijn welkom.
o.d.m@fulladsl.be