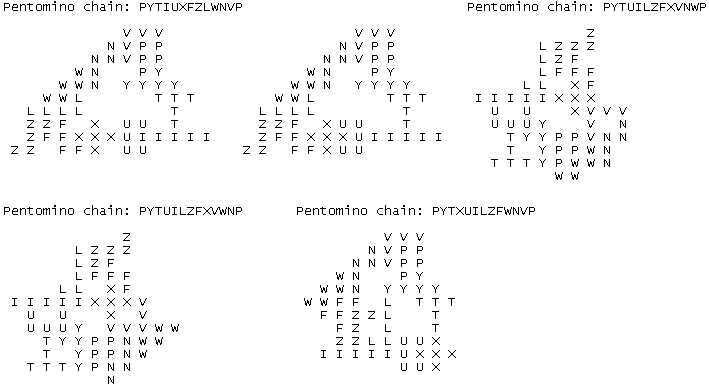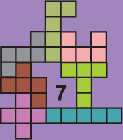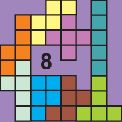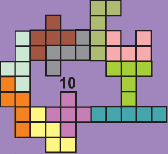|
Onze inspiratie voor de symmetrische ring met 4
pentomino's kwam zowel
van Aad van de Wetering als van Bob Henderson. Bob mailde: "Find a ring of 4 different pentominos that make 4 symmetric pair figures and also make a symmetric ring figure with the same 2 axes of symmetry. I think that you will like my answer, as shown in the 'Lozenge' worksheet. If it were made of gemstones, it would make a pretty piece of jewelry!" En waar haalde Bob zijn inspiraite? In het Bronzen tijdperk, je kan dit zien bij http://www.stone-circles.org.uk/stone/normantondown.htm  |
Aad van de Wetering stuurde het ons toe op zijn manier: het onderwerp van de
mail was 'mooi hé ' en het enige dat in de mail stond was 'woorden
overbodig' Gabriele
Carelli:"Sorry if I wrote you very few mail in last months but I was very busy."
Dat er heel wat geploeterd werd, getuigt de volgende
bijdrage van Philo
TU
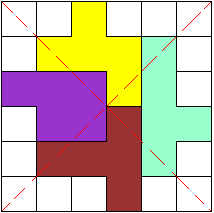
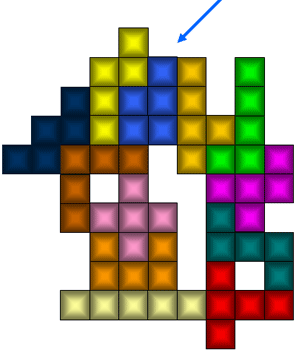
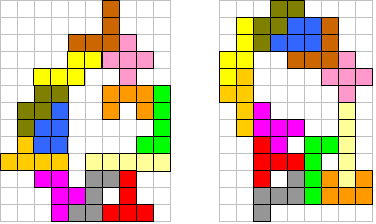
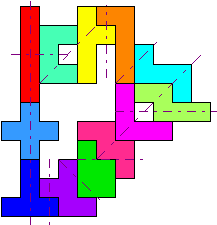
We draaiden de figuur zodat je de intialen van Pieter Torbijn
(PT), aan wie we deze wedstrijd opdragen, beter ziet.
We kregen heel wat berichten van mensen die hun droefheid uitdrukten bij het
heengaan van Pieter Torbijn.
Aad van de Wetering:"Wij zijn er ook
ondersteboven van. Sinds 1991 correspondeerde ik met hem, zijn nauwgezetheid en
humor zal ik erg missen. Ik denk ook dat hij de nieuwe wedstrijd erg mooi
gevonden zou hebben."
"Ja,
het is aan de ene kant jammer dat het idee van de wedstrijd van Stefano is,
aan de andere kant vind ik het zo’n mooi probleem, zoiets kom je maar een
paar keer in de tien jaar tegen. Het is van dezelfde orde als de'narrow
passage' (onze Pieter Torbijn-wedstrijd) zie bijv.
http://www.ericharshbarger.org/pentominoes/article_08.html en
http://www.gamepuzzles.com/tlog/tlog32a.htm
Torbijn was gek op symmetrie, deze opgave had hij werkelijk fantastisch
gevonden. En dat er slechts 21 oplossingen zijn maakt het probleem ook al zo
mooi. Volgens mij ben ik momenteel de enige op de wereld die dit uitgezocht
heeft. Al zal het pakweg Patrick Hamlyn niet veel moeite kosten het mij na
te doen. Op mijn thuispagina ga ik het onderwerp ook aansnijden, natuurlijk
wacht ik tot jouw wedstrijd afgelopen is. Al moet je daar soms wel heel veel
geduld voor hebben…"
Of Patrick Hamlyn dat kan weten we niet, want we hebben niets van hem gekregen.
Aad was echter Bob Henderson en Peter Jeuken vergeten!
We stelden Aads geduld dit keer wel extra op de proef.
Kate Jones:"We
are all very sad that Pieter has passed away. He had some of the greatest ideas
and discoveries for pentominoes and polyforms."
Robert Wainwright:"I corresponded with Torbijn
several years ago on another symmetry problem and was very saddened to learn of
his passing."
Stefano Popovski:"I'm so sorry to hear this
really bad news. Of course this is a great loss and for sure you have my
permission to dedicate the competition to Pieter, we all will miss his articles,
theoretical comments and valuable solutions for so many problems! Whatever you
think would serve to honor such a memorable person will be all right."
Peter Jeuken:"When I heard the news about
Pieter Torbijn I felt very sad and I still do. In the pentomino contest records
one can find many interesting contributions from his hand. Directly coming from
his creative mind. Especially
contest 35 (symmetry from 1 to 12) was a source
of joy for me.
The picture on the pentomino site shows a real gentleman in full concentration.
Three little note pads with different sizes on the table lie exactly
wellorganized on top of each other. Pieter loved symmetry indeed."

Bob Henderson:"I want to find good solutions in
honor of Pieter Torbijn, who was a wonderful puzzle friend."

Dit grapje kregen we van Philo maar het
is wel realiteit want zelfs den Helmut mailt:"I have already found
one solution to the contest. This took a long time. And I am afraid that
I won't have the time to find other solutions. But I'll try."
Het bleef echter bij die ene oplossing.
En Assen Dombev:"I am busy these days, but hope will join next
competition."
Het bleef bij hoop.
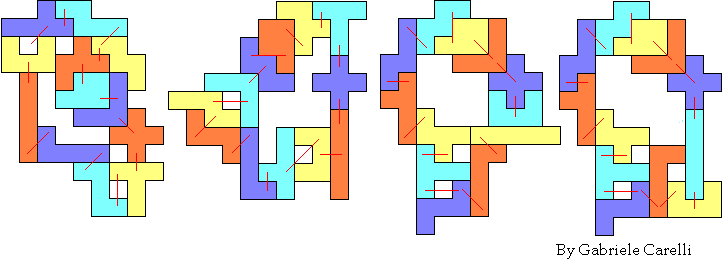
Toch kregen we van Gabriele 4 oplossingen
Als de T de U ontmoet
Is cirkel "rond": Oplossing goed.
(Ik vraag me af: Is er wel één?
Want hierin zie ik echt geen "been")
Ik ben dus lichtelijk "gestoord"
en ploeter nog maar driftig voort…
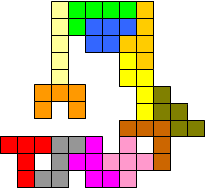
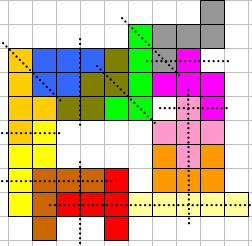
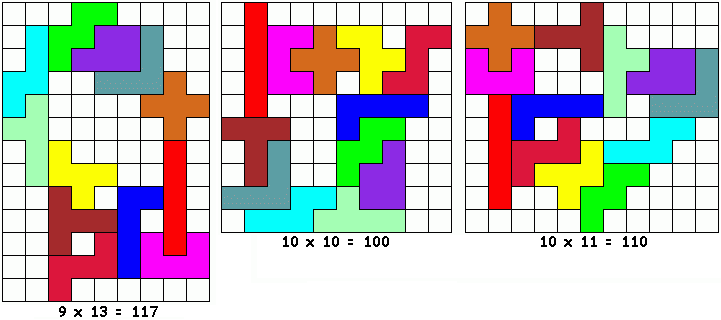
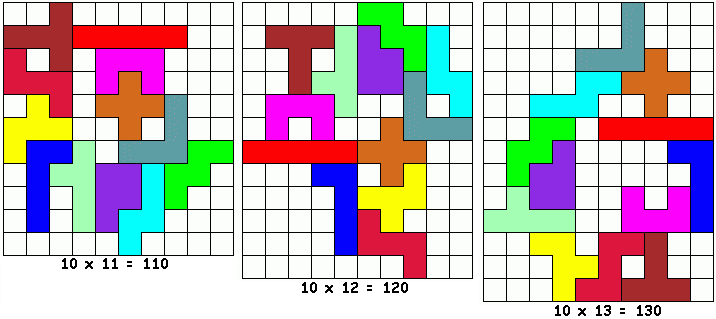
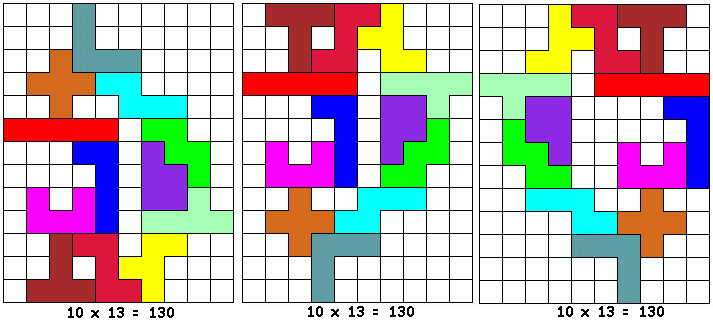
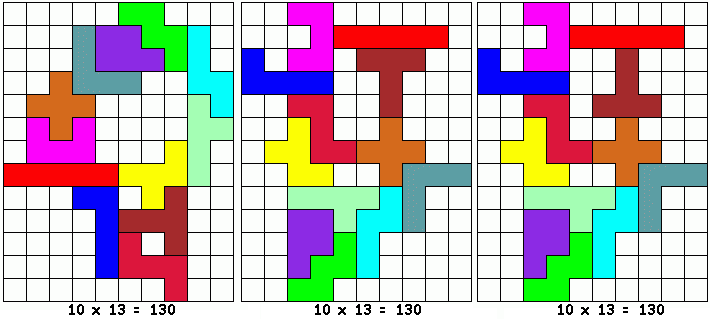
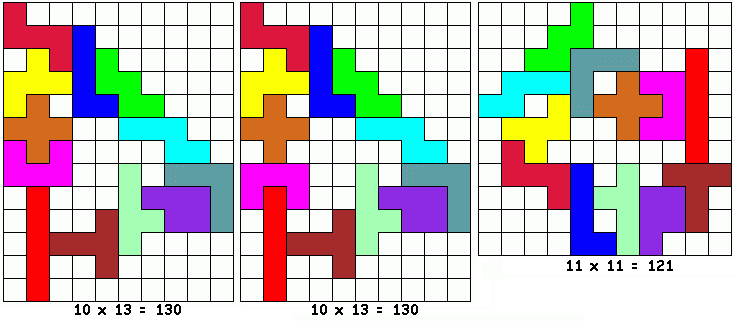
Philo zocht ook naar de kleinste ring met 4 symmetrische paren: LU, UX, XI en IL Een ring met 8 pentomino's De “resten” zijn
symmetrisch! Een ring met 10 pentomino's Er blijft een stoeltje over
om uit rusten voor de ultieme opgave…

We kregen van hem een
prachtige diavoorstelling die je kan downloaden. Hieronder vind je ook een
aantal gifjes uit zijn voorstelling.
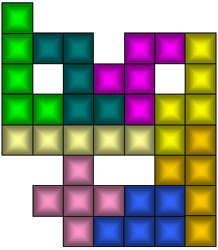
Een grimmig gezicht omdat de oplossing nog niet in zicht is?
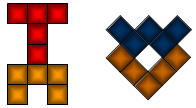
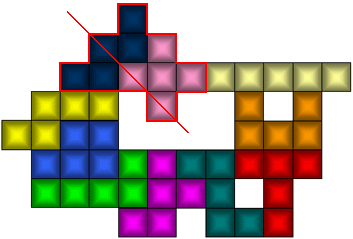
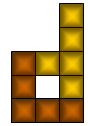
Stefano Popovski mailde:"The solution of Philo with 10 in
the records section is wrong, the W and X are not making any symmetric group in
his solution. Check it again please."
We deden het en hij heeft gelijk. Thanks.
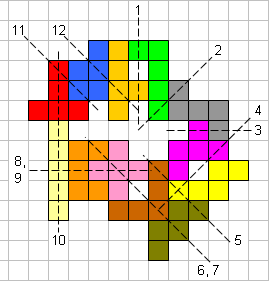
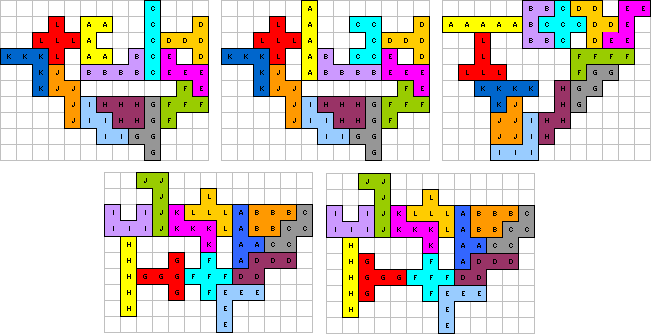
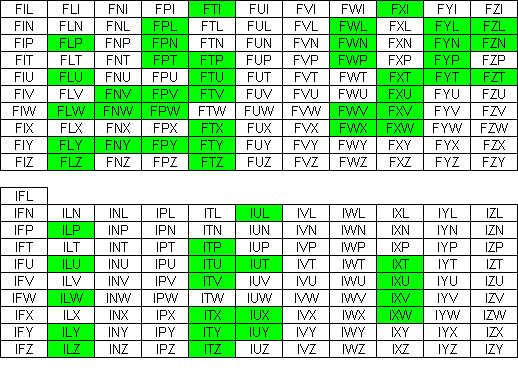
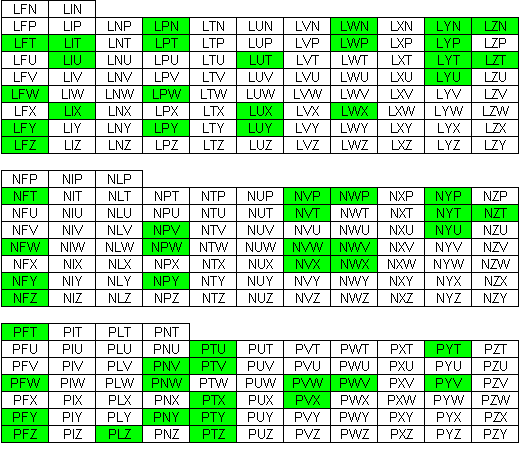
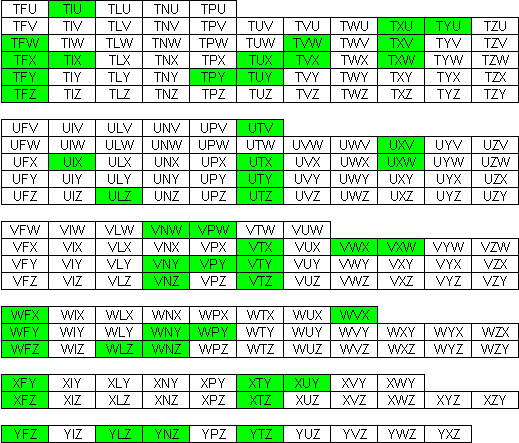
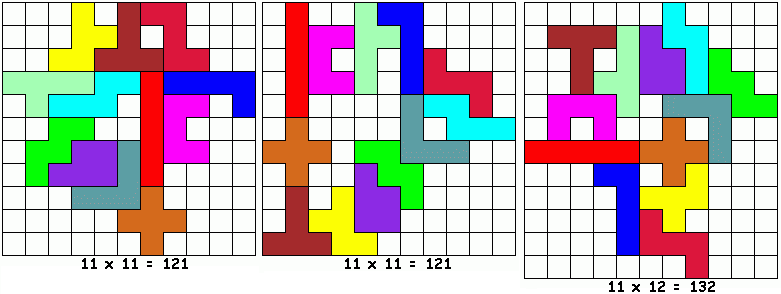
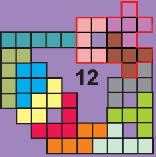
Aad van de Wetering zocht
voor ons de enige ring met 5 symmetrische paren
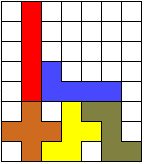
De oplossingen:
|
Philo
(1)
|
||||||||
|
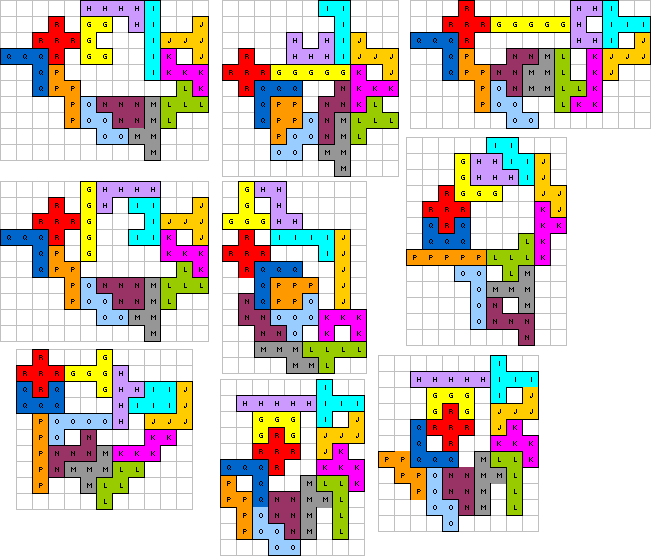
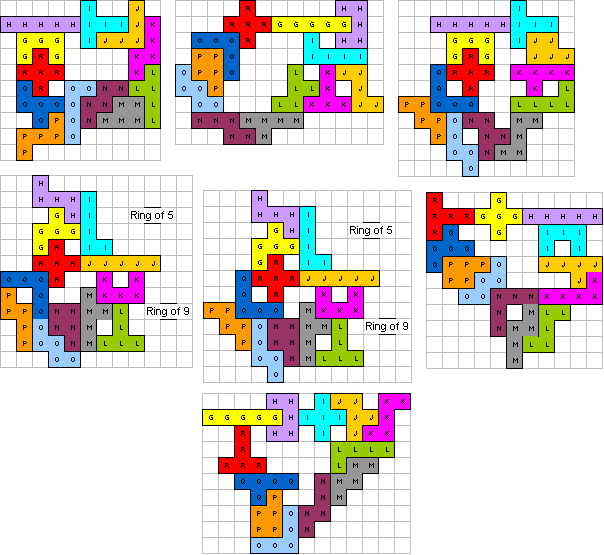
Bob
Henderson
(21)
"Here are 16 new solutions for your new pentomino
competition" |
||||||||
|
Peter
Jeuken (21) |
||||||||
|
Jan
Boogert (1) |
||||||||
|
Annelies Vanneste (2) |
||||||||
|
Edo Timmermans |
||||||||
|
Helmut Postl (1) |
||||||||
|
Gabriele
Carelli (4) |
||||||||
|
Michael
Dowle (1) |
||||||||
|
Robert
Wainwright(1) |
||||||||
|
Aad van de
Wetering (21) |
||||||||
|
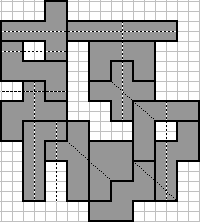
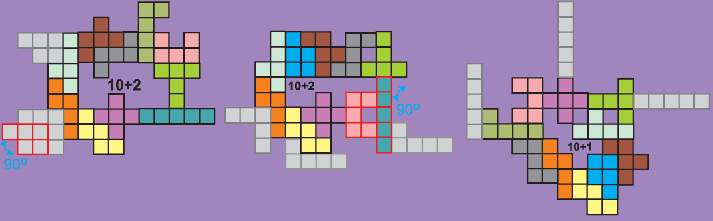
Stefano Popovski
Where it's stated 10+ it means the remaining pentos
can be added at the places marked with pale gray color still
participating in a group, but leaving loose end. |
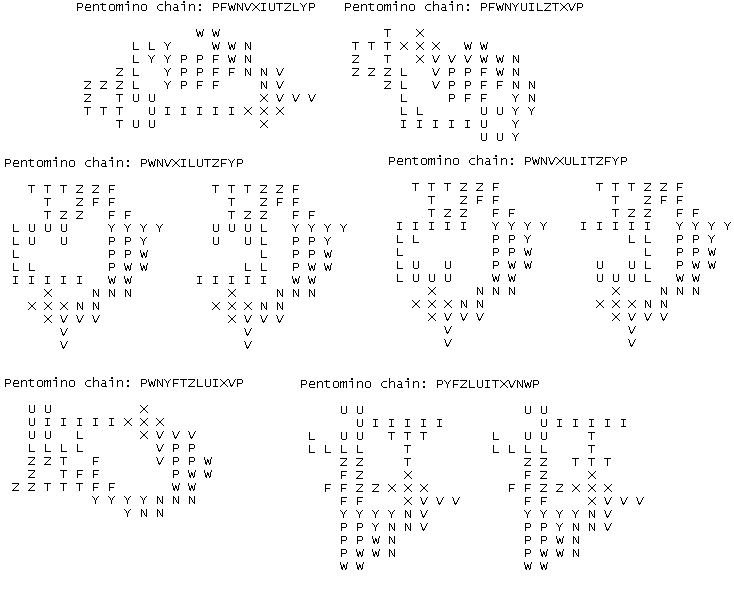
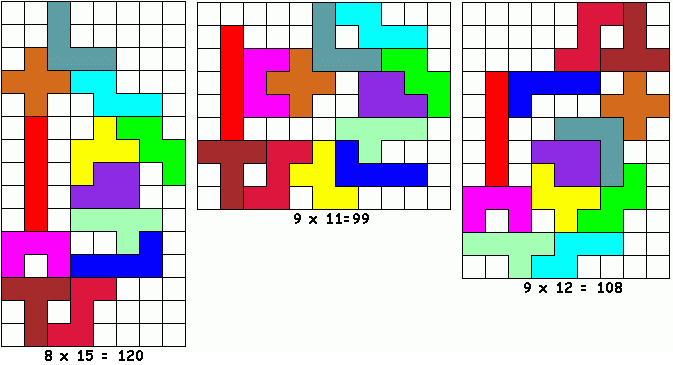
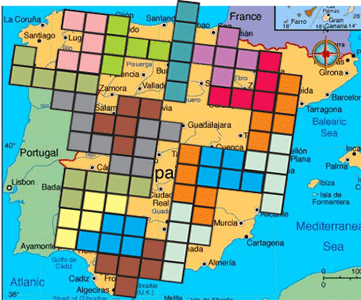
Bob Henderson zocht voor ons een ring met tetromino's en pentomino's zonder parasieten.
Waarschijnlijk naar aanleiding daaarvan mailde op 26 augustus 2008 Aad van de
Wetering:"Zijn de symmetrische combinaties van tetro en pento al bekend?
Gisteren heb ik ze met
Poly3D berekend, ze kwamen er in één keer alle
161 uit. Omdat er
9 zijn met enkel tetro, en
62
met enkel pento, zijn er dus 161 - 9 - 62 = 90 voor tetro+pento."
Er zijn er 72 met een symmetrie-as en 18 met een symmetriemiddelpunt.
Je kan bij symmetrie een
overzicht vinden.
Geniet ervan:

Maar er kwam meer.
"More tetro+pento chains are shown in the attached file, many with no parasites!
I told my solver that each new piece must not touch the ones placed 2 or 3 steps
earlier. Of course, it must still touch the one placed just before it, making a
symmetrical pair."
Van de nieuwe 134 oplossingen waren er 23 zonder parasieten. De vorige
oplossing is dus helemaal niet uniek :-(
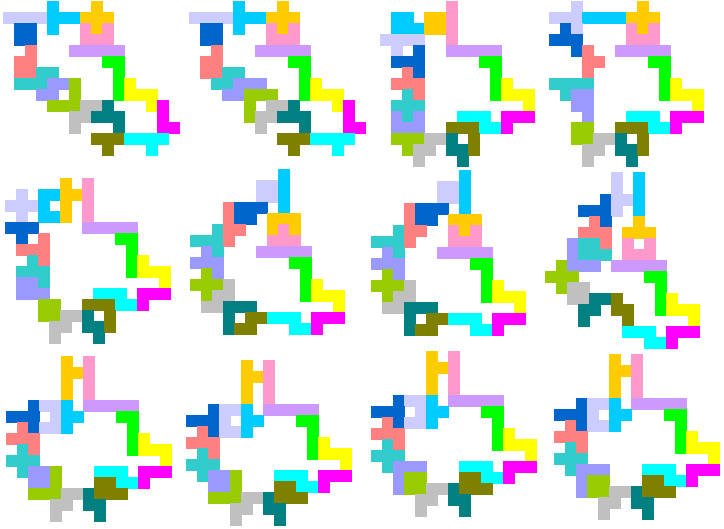
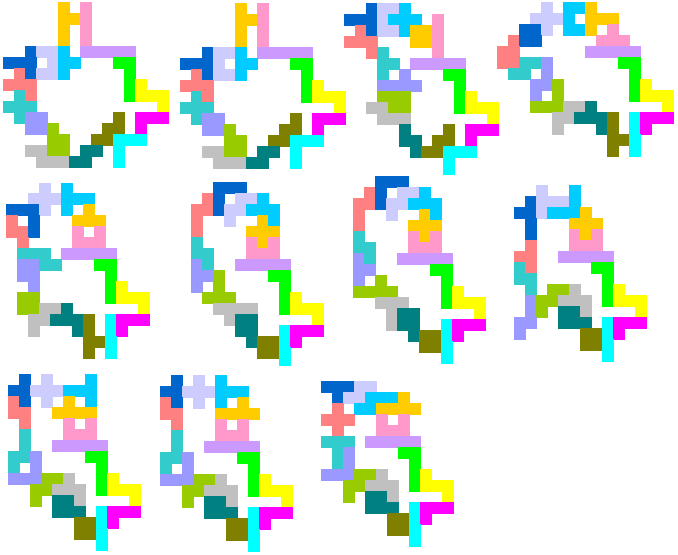
"I am running the same logic for the one-sided pentominoes now. I expect that
many more of these chains will also be found with no parasites."
En dat was ook zo . Hij stuurde ons 16 oplossingen.
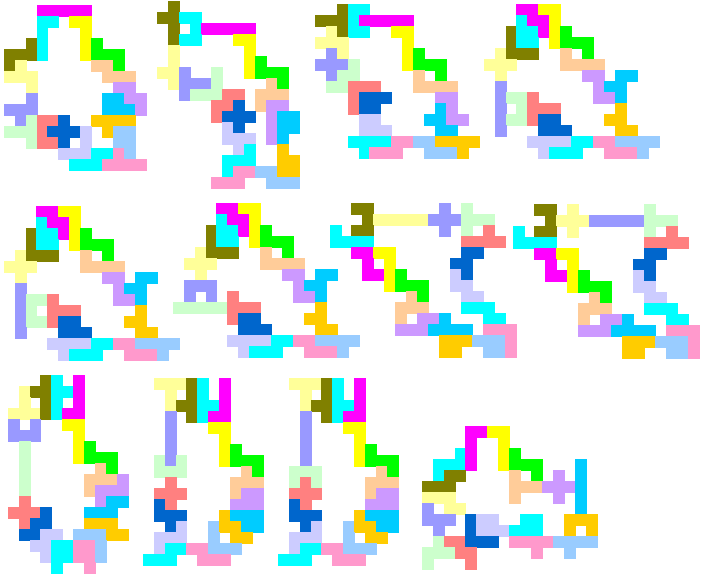
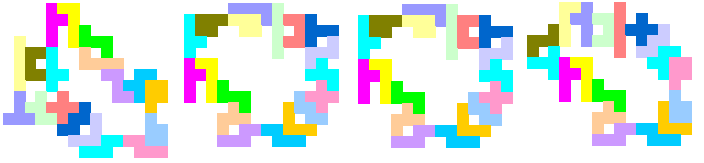
Bij vaststelling van fouten of onvolledigheid, mail
naar: