Pentomino,
tetromino's en symmetrie
Naar aanleiding van wedstrijd 37
zocht Bob Henderson ook symmetrische kettingen bestaande uit tetromino's en
pentomino's.
Je kan het vinden bij
records.
Op 26 augustus 2008 kregen we een mail van Aad van de Wetering:"Zijn de
symmetrische combinaties van tetro en pento al bekend? Gisteren heb ik ze
met
Poly3D berekend, ze kwamen er in één keer
alle 161 uit. Omdat er 9 zijn
met enkel tetro, en 62 met enkel pento, zijn er dus 161 - 9 - 62
= 90 voor tetro+pento."
Er zijn er 72 met een symmetrie-as en 18 met een symmetriemiddelpunt.
Aad maakte dit onderscheid niet:"Elke figuur die na draaien en/of
spiegelen hetzelfde origineel oplevert is symmetrisch."
Juist natuurlijk maar we maken wel onderscheid.
Figuren bestaande uit een pentomino en een tetromino die een
symmetrie-as bezitten.
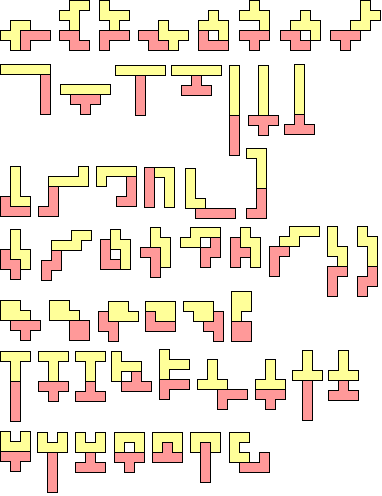
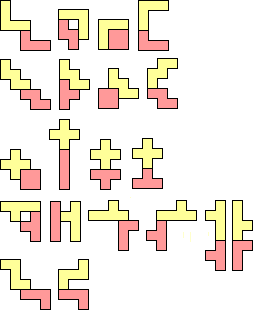
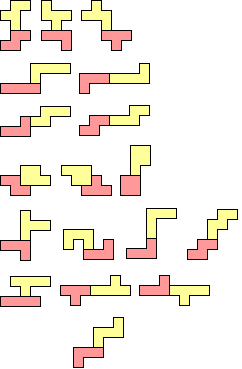
Figuren bestaande uit een pentomino en een tetromino die een
symmetrie-middelpunt bezitten.
Commentaar is welkom.
o.d.m@fulladsl.be
