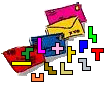
Aangezien vier pentomino's samen een oppervlakte 20 hebben moeten we een vierkant maken met oppervlakte 20.
We kunnen 20 bekomen als de som van de kwadraten van 2 en 4. Dus als we een rechthoekige driehoek hebben met rechthoekszijden 2 en 4 dan is de schuine zijde ook de zijde van een vierkant met oppervlakte 20. Bij de pentomino's vinden we echter geen rechthoekige driehoeken met rechthoekszijden 2 en 4.
Daarom vereenvoudigen we de vierkantswortel:
Onderstaand gif komt uit onze syllabus van NWD 2002 maar dit versneden pintje in 8 stukken werd ons oorspronkelijk aangeboden door Aad van de Wetering.
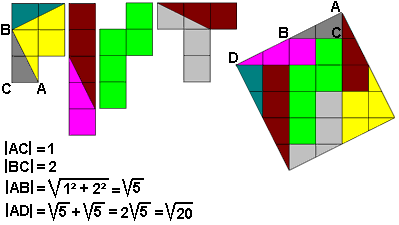
Katrijn Cierkens versneed voor ons een 'zuil' in 10 stukken.
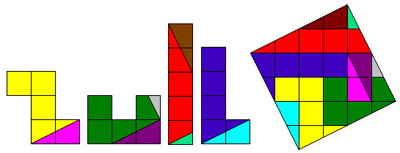
We kunnen de zuil versnijden in 9 stukken.
Kan je dat ook?
Oplossing
We hebben hier ook een geogebra animatie van
We kunnen ook een 'tulp' versnijden in 8 stukken.(met dank aan Aad)
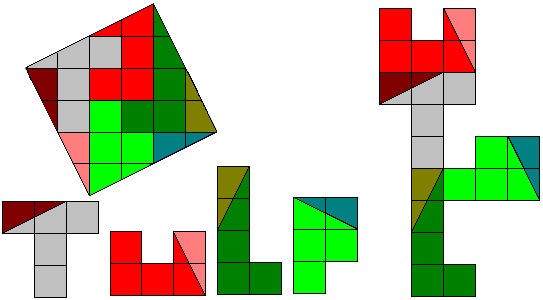
We kunnen ook een 'tuil' versnijden in 9 stukken
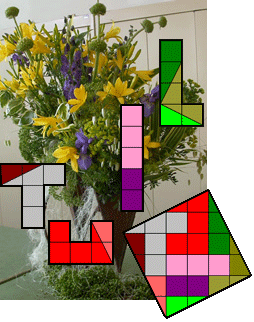
'Tuil' kan ook tot vierkant in 8 stukken.
Kan je dat ook?
Oplossing
We hebben er ook een mooie geogebra animatie van.
We hebben met geogebra ook een
animatie gemaakt van
4
F-pentomino's tot een vierkant,
4
I-pentominono's tot een vierkant,van
4 P-pentomino's tot een vierkant en van
4 W-pentomino's tot een vierkant.
Op aanvraag versneed Aad van de Wetering een 'TUTU' voor ons in acht stukken. De
figuur in het vierkant heeft een symmetriemiddelpunt. Mooi!
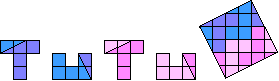
We hebben er ook een
geogebra animatie van.
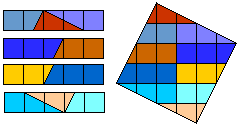
Helmut Postl versneed voor ons telkens 4 gelijke pentomino's tot een vierkant.
Dit zijn de minimale aantal stukken:
F:8, I:10, L:8, N:8, P:8, T:9, U:10, V:8, W:10, X:9, Y:8, Z:8.
Vooral de X in 9 stukken vinden we heel knap gevonden!
Als je geen kleur bezit om af te drukken, kan je op het gif drukken en dan krijg
je de verdeling zonder ruitjes.
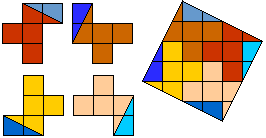 |
 |
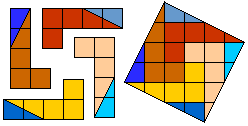 |
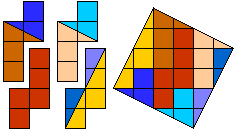 |
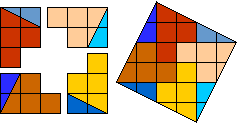 |
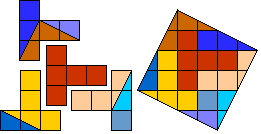 |
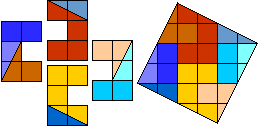 |
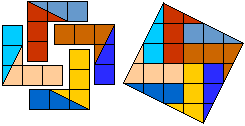 |
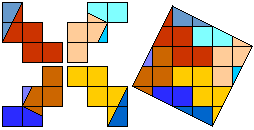 |
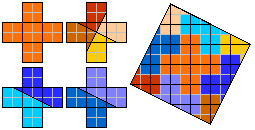 |
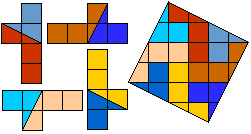 |
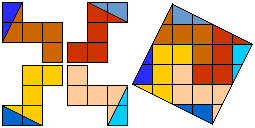 |
We willen heel graag andere versnijdingen toevoegen
Mail naar
o.d.m@fulladsl.be