De aanleiding tot de publicatie van deze pagina is het interessante blog van Luc Gheysens waar we het volgende vonden:
Hieronder zie je meteen mijn favoriete puzzel uit het boek 'Sam Loyd's Cyclopedia of Puzzles'.
Je vindt deze puzzels nu online op
http://www.jwstelly.org/CyclopediaOfPuzzles/CyclopediaOfPuzzles.php.
Luc stelde voor:"Als je jouw leerlingen wilt laten kennismaken met verschillende vlakke meetkundige figuren dan zal deze puzzel zeker een uitdaging vormen."
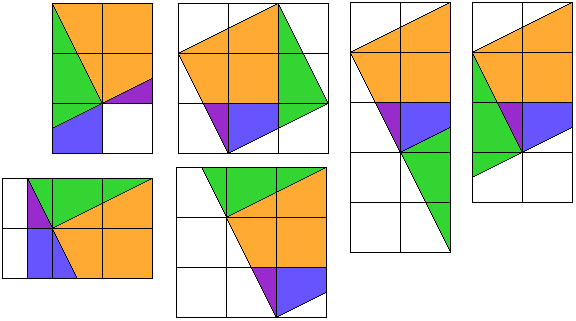
We maakten een tekening van de 5 stukken die je hier kan downloaden (als gif, mooi om af te drukken)

De uitdaging bestaat er nu in met deze 5 puzzelstukjes achtereenvolgens een kruis, een vierkant, een rechthoekige driehoek, een parallellogram,een rechthoek en een veelhoek te vormen.
We waren deze puzzel al eerder tegengekomen, maar we zagen het Grieks kruis als X-pentomino.

In het prachtig boek van Moscovich is dit puzzel is dit nr. 476 (van de 1000) maar tot een rechthoek staat er niet bij.
Het X-kruis versnijden tot vierkant kan je vinden bij versnijdingen van 1 pentomino tot vierkant.
Aangezien een pentomino een oppervlakte 5 heeft moet het vierkant oppervlakte 5 hebben.
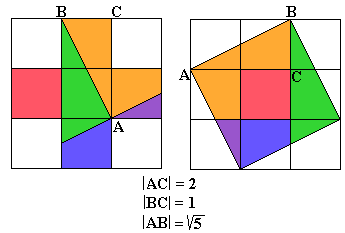
We kunnen 5 bekomen als de som van de kwadraten van 1 en 2. Dus als we een rechthoekige driehoek hebben met rechthoekszijden 1 en 2 dan is de schuine zijde ook de zijde van een vierkant met oppervlakte 5.
De andere figuren hebben ook oppervlakte 5
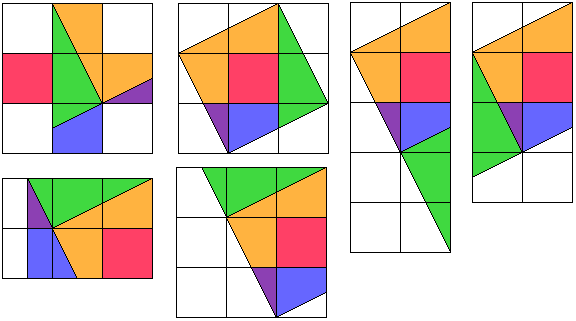
We hebben met geogebra ook een animatie gemaakt.
Maken van de X-pentomino tot vierkant, rechthoekige driehoek, parallellogram, rechthoek en veelhoek
Van X-pentomino naar rechthoek
We willen heel graag opmerkingen of
aanvullingen toevoegen.
Mail naar
o.d.m@fulladsl.be
We kregen al een paar opmerkingen:
Door het rode vierkant te verplaatsen kunnen we dat voor elke pentomino.
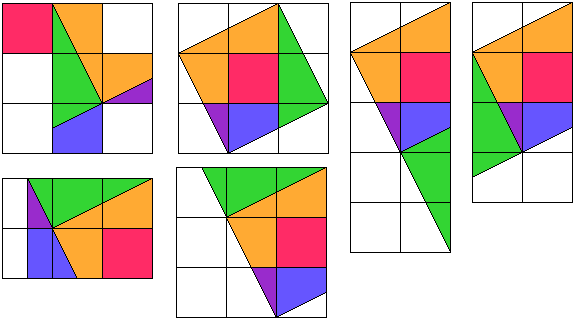
Voor de P-pentomino kan het ook in 4 stukken.