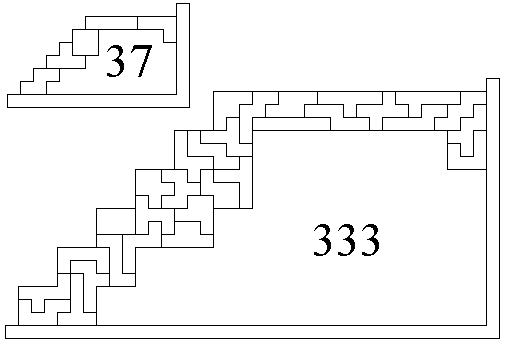
Voor het maken van de treden heeft men 4 mogelijkheden.
Voor de overloop heeft men 3 mogelijkheden. Er zijn dus 12 mogelijkheden voor de tetrotrap.
Brendan Owen uit AustraliŽ mailde ons voor elke mogelijkheid een vergrote oplossing.![]()
![]()
Met FLatpoly2 zochten we telkens het aantal mogelijke oplossingen bij elk geval.
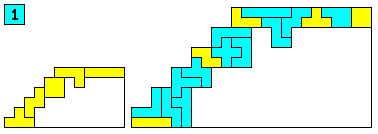
Aantal oplossingen: 70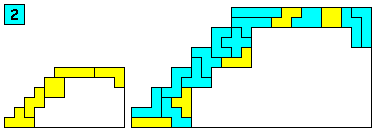
Aantal oplossingen: 139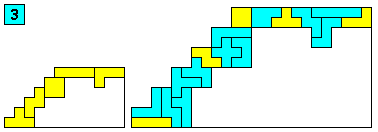
Aantal oplossingen: 82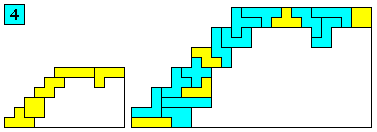
Aantal oplossingen: 191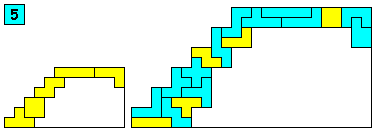
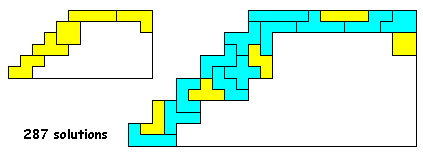
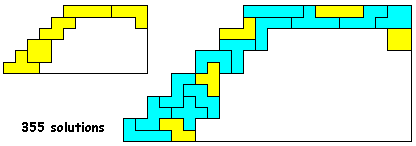
Aantal oplossingen: 355
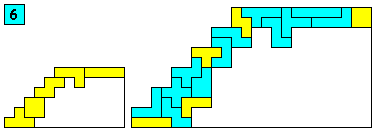
Aantal oplossingen: 265
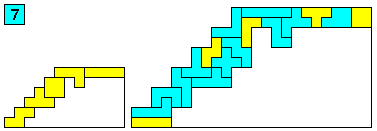
Aantal oplossingen: 146
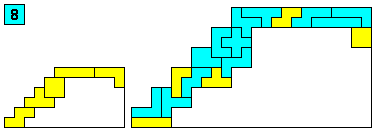
Aantal oplossingen: 287
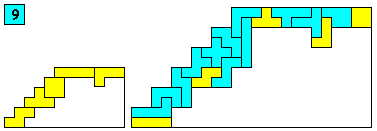
Aantal oplossingen: 199
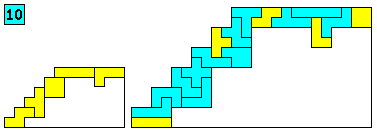
Aantal oplossingen: 151
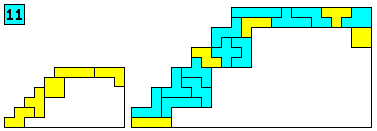
Aantal oplossingen: 247
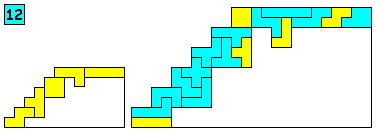
Aantal oplossingen: 134
| Naam | Herkomst | Oplossing |
| Bob Allen | USA | 2 |
| Tom Caekebeke | BelgiŽ | 7 |
| Kate Jones | USA | 7 |
| Gabriele Carelli | ItaliŽ | 1,6,7 en 12 |
| Joseph De Vincentis | USA | 8 |
| Nisrine El Ahmadi | BelgiŽ | 6 |
| Patricia Etcheverry | ArgentiniŽ | 5 en 11 |
| Dion Gijswijt | Nederland | 12 |
| Patrick Hamlyn | Australia | 5 |
| Bob Henderson | USA | 5 |
| Michael Keller | USA | 8 |
| Brendan Owen | AustraliŽ | 1 tot 12 |
| Stefano Popovski | Bulgarije | 2 en 5 |
| Helmut Postl | Oostenrijk | 5 |
| Sasha Ravsky | Rusland | 5 |
| Andreas Rottler | Duitsland | 2 |
| Timoty Snauwaert | BelgiŽ | 8 |
| Sergio Stanzani | ItaliŽ | 3 |
| Pieter Torbijn | Nederland | 3 |
| Dario Uri | ItaliŽ | 1 |
| B.J. van der Zwaag | Nederland | 1 tot 12 |
| Aad v.d.Wetering | Nederland | 10 |
Berend Jan van der Zwaag mailde:"Erg leuke site hebben jullie, mijn complimenten! Zijn volgende oplossing is nog leuker omdat elke pentomino juist 1 tetromino raakt. Van Michael Keller kregen we ook een trap op schaal 3. Van Patrick Hamlyn kregen we allle mogelijke trappen met tetromino's toegemaild.Als we eens veel tijd hebben zullen we ze op de site plaatsen.
Zijn deze records onjuist of onvolledig,
mail het ons.
Aad van de Weterings programma is voor de opdrachten en de wedstrijd
inderdaad een ontzettend handig stukje gereedschap.
Wat betreft de tetrotrapwedstrijd (leuke wedstrijd!) kom ik tot een
maximale ruimte van 37 onder de kleine trap.
Ik heb ook meteen maar even geteld hoeveel oplossingen er zijn.Als ik goed geteld heb zijn dat er 2266, verdeeld over 12 verschillende configuraties voor de kleine trap.Sommige oplossingen zijn extra interessant, omdat daar in de grote trap de tetromino's niet slechts elkaar niet raken, maar er bovendien tussen
de tetromino's steeds tenminste twee pentomino's zitten, oftewel geen enkele pentomino raakt twee tetromino's."
Hij vulde hem op met 30 van de 35 hexomino's.