Records Wedstrijd 41

 Edo Timmermans zorgde voor deze mooie maar moeilijke opgave.

Hij stuurde zelf een voorstel in.  

Er kwamen maar 5 andere tuinmannen met een voorstel.


Bob Henderson mailde:"Please show the drawings to Count Penteviticole so that he can choose the best design for his island in a lake surrounded by vinyards. It is clear that the smallest possible island perimeter is 32, because the 60 units of area in the 12 pentominos can not be contained inside any rectangle smaller than 8x8, 9x7, or 10x6 units, each of which has a perimeter of 32 units. My result for the largest island perimeter is 72 units, but if the Count would like to have a large pond or 2 small ponds on his island, the net island perimeter including the edges of these ponds can be increased to 74 or 76 units."
Wat is die Bob toch altijd vindingrijk maar de graaf wil geen extra kosten maken voor een brug!
 

Min: 32   Max: 72 74 76

Peter Jeuken mailde een gesprek tussen twee tuinontwerpers, TO1 en TO2
TO1:Ben je al een beetje opgeschoten met het tuinontwerp voor graaf Penteviticole?
TO2:Blij dat je het vraagt. Want ik ben net klaar met het ontwerp van een eiland met de kleinst mogelijke omtrek. De omtrek van het eiland is 32. Kijk maar.

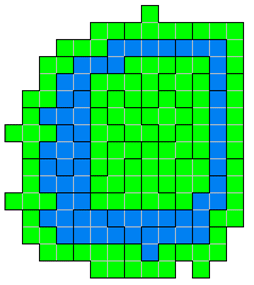
TO1: Ziet er goed uit. Volgens mij is 32 het theoretisch minimum. De graaf zal tevreden zijn.
Maar ik heb ook niet stil gezeten. Ik heb mij bezig gehouden met het ontwerp van een eiland met de maximale omtrek. Mijn eerste een oplossing had een omtrek van 64. Later ben ik uitgekomen op 68.

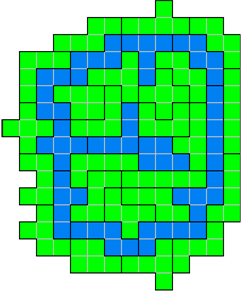
Zoals je ziet is er veel extra omtrek ontstaan door de stukjes P en V die een diepe inham in het eiland vormen.
TO2: Wat een wonderlijke vorm. Als je goed kijkt wordt door de inham het eiland in drie schiereilanden opgedeeld. Een met PTV, een met UWXY en een met FILNZ. Dat zal de graaf bevallen. Hij kan de verschillende soorten rozen op verschillende schiereilanden onderbrengen.
Nog even terugkomen op die PV combinatie. Ik geloof dat ik een idee heb. Wat zou er gebeuren als je die combinatie zodanig verplaatst dat hij nergens de waterrand raakt? Juist, dan ontstaat er een vijver op het eiland. Water dat eerst de tuin omsloot verandert in water dat door de tuin wordt ingesloten. Wat óók verandert is de omtrek van het eiland. Die wordt dan 50 en de omtrek van de vijver is 20. De omtrek van het eiland is afgenomen. Maar wat is er gebeurd met de totale oeverlengte? Die is toegenomen van 68 naar 70!
TO1: Volgens mij heb je helemaal gelijk. Wacht eens even... Je brengt me op een idee. Als het mogelijk is om P en V aparte vijvers te laten vormen, wordt de totale oeverlengte zelfs 72. Ik zie het helemaal voor me. Kijk maar mee.

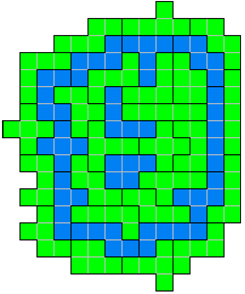
TO2:Volkomen juist. Maar het is de vraag waar de graaf aan dacht toen hij sprak over maximale omtrek. Als hij dat in letterlijke zin bedoelde is deze oplossing minder goed, maar als hij doelde op maximale oeverlengte is deze oplossing gunstiger.
TO1: Ik kan toch ook beide oplossingen insturen. Laat hem zelf maar kiezen. Persoonlijk vind ik de laatste de mooiste. Een wijngaard die een meer insluit, een meer dat een rozentuin insluit en tenslotte een rozentuin die twee vijvers insluit. En als de graaf wil vissen hoeft hij niet persé naar de rand van zijn eiland te gaan maar kan hij ook midden op het eiland blijven.
T02: In al je geestdrift ben je vergeten dat jouw ontwerp maar één van de twee vragen beantwoordt. Maar samen met mijn ontwerp hebben we een complete oplossing. Laten we die combineren. Indien onze gezamenlijke inzending wint, eten we het eiland van chocolade samen op.
T01: Dat is een prima plan.

Het was niet het beste plan maar het werd bekroond. Graven zijn ondoorgrondelijk ;-)



Helmut Postl stuurde een mooi bewijs dat 72 de max is.
"I assume now that the lake must be a ring where the pentominoes must touch with at least one side.

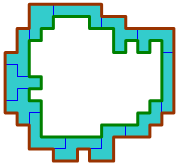
Each pentomino has a perimeter of 12 except the P which has 10. The sum of all pentomino perimeters therefore is 142. This value can also be seen as sum of the brown line, the green line and twice the short blue lines. The brown line is the outer perimeter of the lake, the green line is the perimeter of the island, and the short blue lines are the touch lines of the pentominoes.
Length of the short blue lines: Since there are 12 blue lines which have at least length 1, the sum of the blue lines is at least 12.
Length of the brown line: This line surrounds an area of 120 (two sets of pentominoes). Each such area has a perimeter of at least 44. The only minimum examples are a 10x12-rectangle and a 11x11-square with one corner cell omitted.
The length of the green line is therefore 142 minus brown line minus twice blue lines ≥ 142 – 44 – 2∙12 = 74.
So the maximal island perimeter can be no more than 74. In this case the brown line can only be the perimeter of one of the two areas described above, and one can see that this cannot be achieved. Since odd perimeters are not possible, the next candidate is 72. And as seen, this is possible.
A perimeter of 76 can therefore only be achieved if the assumption is dropped that the pentominoes must touch along sides. And strictly speaking, I don’t read this condition from the contest text. So it may be allowed that the pentominoes touch also only at corners. But from my feeling, I won’t then call the inner region an „island“ since it also touches the outer vineyard area. Still another possibility might be that the pentominoes are shifted against each other by a fraction of a side (which may result in small holes inside the island). This is also not explicitely ruled out, and maybe this will yield a possible solution. I don’t see other possibilities at the moment."

 

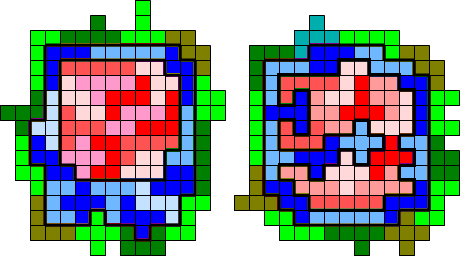
Livio Zucca mailde:"I send you my solution. It isn't a record, is a 'by hand' solution on the beach. It's made with the spirit of de Coubertin :o)"

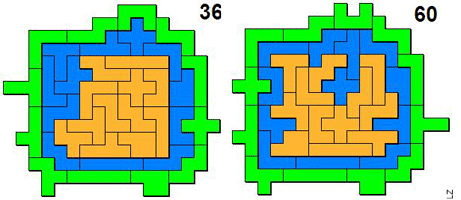
Aad van de Wetering;"Zo gemakkelijk als de kleine oplossing ging, zo moeilijk ging de grote. Steeds was ik er bijna, steeds ging het net niet. Maar nu is de 72 eindelijk bereikt.
Nu nog maar eens zien wie er minder dan 32 dan wel meer dan 72 weten te halen, je weet maar nooit tenslotte."
Maar Aad weet het meestal wel!

Deze keer kregen we ook een mail van Junk Kato: "It's a very interesting problem.
I have no time to solve it. Sorry. I think minimum answer be 32. I don'nt know maximum answer."

 Bij vaststelling van fouten of onvolledigheid, mail naar: