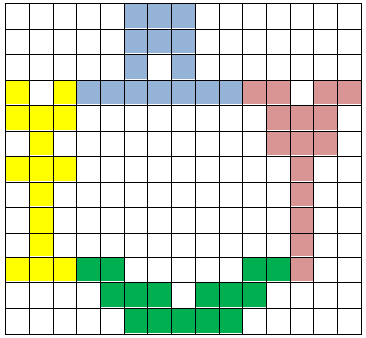
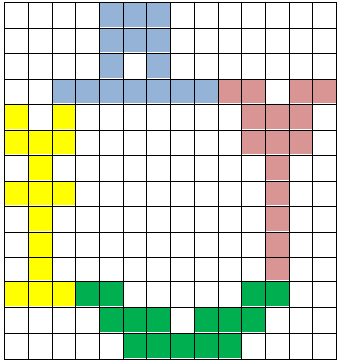
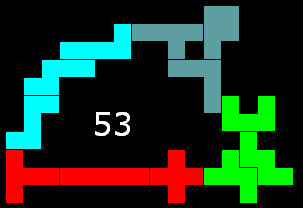
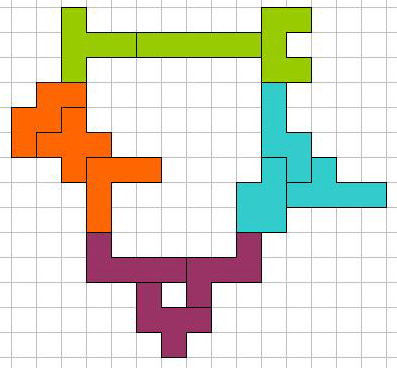Bob Henderson uit USA wenste ons: "Happy Easter" met zijn inzending.
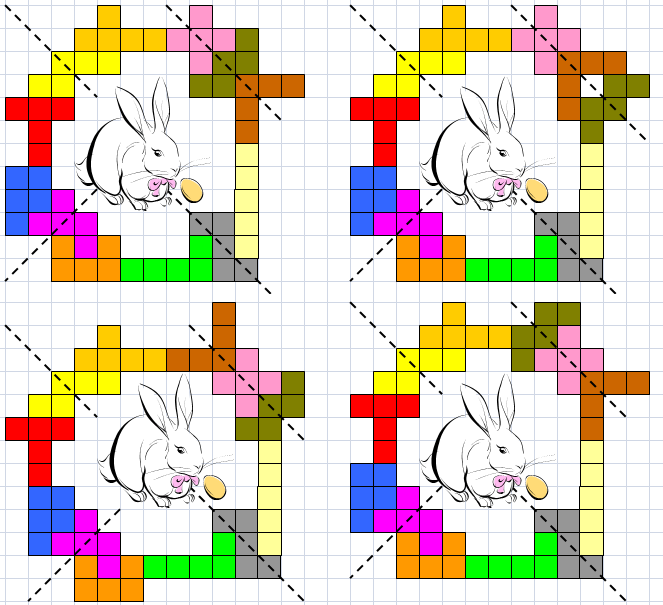
Hij had een omsluiting van 53 eenheden.
We kregen van Bob een maximale inzending (dat denken we toch)
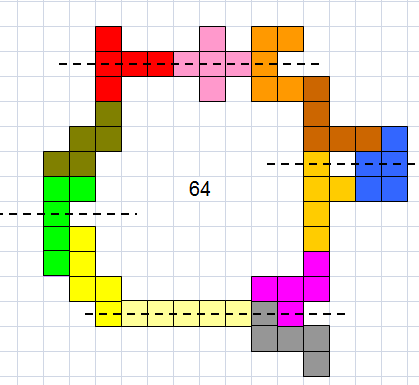
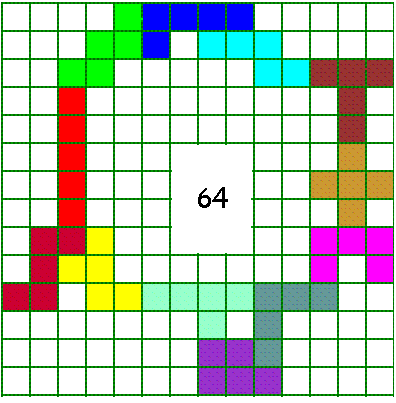
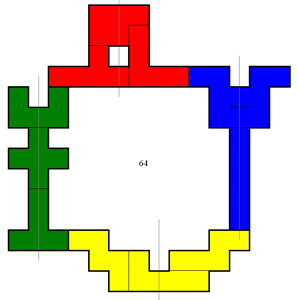
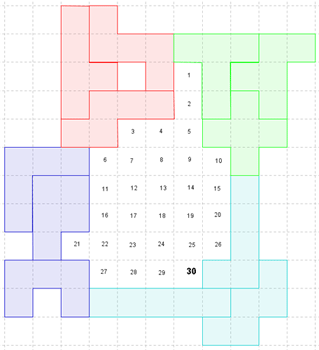
Van Helmut Postl (Oostenrijk) kregen we ook een omsluiting van 64.
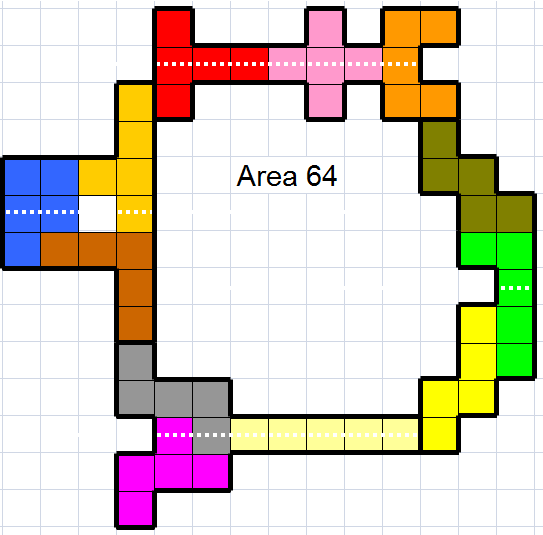
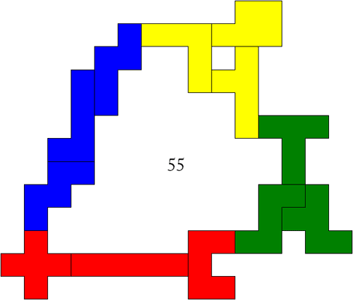
Van Aad Thoen (Nederland) kregen we eerst de volgende commentaar: "Ik heb de nieuwe wedstrijd bekeken. Die symmetrische vormen in het voorbeeld zien er mooi uit. Daar ligt mijns inziens de hele moeilijkheid. Twee symmetrische vormen vallen wel rap te maken. Maar dan: met het restant lukt dat nauwelijks. Symmetrie met een diagonale as is ook al niet eenvoudig. Kortom: dit is een moeilijke puzzel!!"
"Symmphilo heeft me razend veel geholpen, dank u. Wat waanzinnig veel symmetrische trio's staan daar. Degene die ze heeft ingevoerd
verdient een 1ste-rangs plaats in de pentominohemel! Voor ik symmphilo raadpleegde had ik zelf een handjevol trio's gevonden. Nu voel ik me een uitslover met te vertellen dat de volgende vier daarvan niet op symmphilo staan."
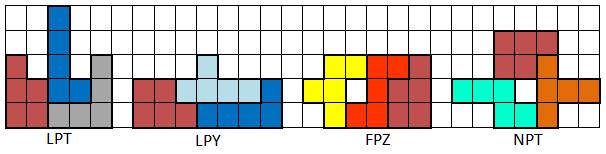
Op symmphilo staan inderdaad alleen de trio's die 2 per 2 een symmetrie-as hebben.
"Mijn inschatting is dat de score niet boven het huidige wedstrijdnummer (48) kan uitkomen."
We kregen echter een oplossing van 62.
En met een beetje schuifwerk werd het 64!