50. Jubileum- wedstrijd
Met heel veel dank voor alle mooie problemen die we kregen.
Daarom dachten we dat we de oplosser zelf laten kiezen.
We hopen dat we niemand vergeten zijn. Stuur anders een mail.
Dit wordt waarschijnlijk onze laatste wedstrijd.
We beginnen met de opgave van Kate Jones want we kregen de volgende mail: "Attached is a "50" puzzle I designed some time ago, one copy of which we will be happy to give as a prize for your winner. It is a $45 value and contains all the polyominoes 1 through 5. It has many solutions and is based on our Poly-5 puzzle, www.gamepuzzles.com/polycub2.htm#P5"

We danken Kate en Kadon Enterprises voor de prijs.
Opgave van
Kate Jones.

Vul het getal 50 op met de 12 pentomino's, de 5 tetromino's,
de 2 trominoes, de domino en de monomino.
De tetromino's, de tromino's, de domino en de monomino mogen elkaar niet
raken, ook niet in de hoekpunten.
Kate wil ook weten of je het zelf opgelost hebt of het laten oplossen
hebt door de computer.
Om dit zelf op te lossen maakten we een
exelbestand
en ook een
geogebrabestand.
Als deze niet duidelijk zijn kan je altijd uitleg krijgen
o.d.m@fulladsl.be
FlatPoly berekende dat er heel wat verschillende oplossingen zijn.
Je kan Flatpoly downloaden op
http://home.wxs.nl/~avdw3b/aad.html

Van Kate Jones was ook het idee van onze
34ste wedstrijd
Opgave van Bob Harris
(A) Kies een pentomino en maak er 13 kopies van (gele kleur) en kies een
tetromino en maak er 4 kopies van (zwarte kleur).
(B) Plaats de stukken zodat die een vierkant van 7x7 vullen. De gele
stukken zijn "positief" en +1 waard; de zwarte stukken zijn "negatief"
en -1 waard. De zwarte stukken komen op de gele te liggen.
Het is ook mogelijk van een pentominoset te nemen en een extra pentomino
i.p.v. 13 kopies van dezelfde pentomino en een tetrominoset met één
tetromino eruit naar keuze.
Het idee:
http://www.bumblebeagle.org/polycubes/7andF.solution.gif
De vraag was toen: maak een 4x4x4 kubus met kopies van een heptakubus en
een pentakubus. Hoeveel kopies van elke soort heeft men nodig? We lossen
op: 7a + 5b = 64 waarbij a en b natuurlijke getallen zijn. De
oplossingen zijn: a=2 en b=10 en ook a=7 en b=3.
Het huidige probleem is in het vlak: een vierkant van 7x7 vullen met
pentomino's and tetromino's. We lossen op: 5a+4b = 49 waarbij a en b
natuurlijke getallen zijn. De oplossingen zijn (9,1), (5,6), (1,11). Er
zijn echter meer oplossingen als a en b gehele getallen mogen zijn. Een
voorbeeld is (a,b) = (13,-4) dus 13 pentomino's en 4 negatieve
tetromino's.
In ons voorbeeld kozen we voor de L-pentomino en de L-tetromino.
Ga met de muisaanwijzer over de tekening.

Kan je het met de andere pentomino's ?
Opgave van
Martin Watson.
Martin Watson gaf ons ook het idee van onze
21 ste wedstrijd.
Plaats de 12 pentomino's in een vierkant van 12x12 zodat ze elkaar niet
raken, ook niet in de hoekpunten.
Tel het aantal eenheden van de pentomino's die op de zijden van het
vierkant gelegen zijn.
Probeer zowel een minimum als een maximum te vinden.
In het voorbeeld is het aantal 32.
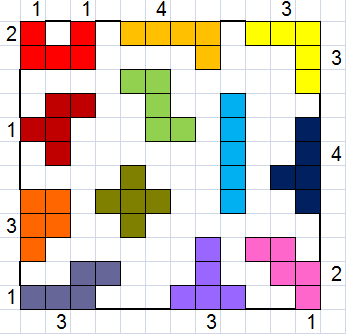
Opgave van Peter Jeuken
Speciaal voor ons bedacht Peter deze pentominupuzzel.
12
sets van 12 pentomino’s en 12 sets van 5 tetromino’s vormen samen een
32x32 vierkant waarvan de 4 hoeken (4x4 vierkanten) ontbreken.
Zie je het liever iets groter, druk dan op het gif.

Knip de figuur in 12 stukken en wel zodanig dat ieder stuk precies 12
verschillende pentomino’s en 5 verschillende tetromino’s bevat.
Er mag alleen langs het raster worden geknipt. Pentomino’s en
tetromino’s mogen niet worden doorgeknipt.
Indien er meer dan één oplossing is, geldt de oplossing met de kleinste
totale omtrek van de 12 stukken.
Opgave van Aad Thoen :
Pentomino-eilandjes
Leg alle pentomino’s als eilandjes in een zee, de zee dient zo
klein mogelijk te zijn.
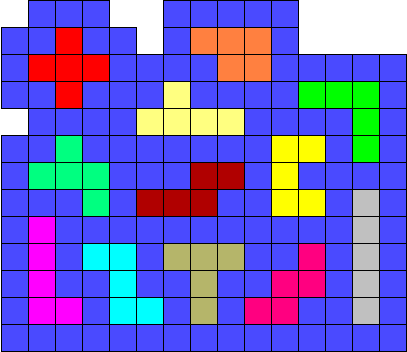
In ons voorbeeld is de zee 122 eenheden.
Een variant op dit probleem is ons
potpourriprobleem 11 waarbij de zee een
rechthoek moest zijn.
Een ander probleem is dat we toestaan dat de pentomino's schiereilandjes
zijn.
Met bijkomende voorwaarde dat de vorm van de zee een rechthoek is vind
je dit besproken in
potporriprobleem 12
Opgave van Aad van de Wetering
Aad van de Wetering heeft onze pentomionosite groot gemaakt,
waarvoor heel veel dank.
1 + 1 = 3
Dit probleem was van onze overleden vriend Pieter
Torbijn waaraan we de hele wedstrijd opdragen.
Omsluit een pentominoset met twee andere sets. Maak de omgesloten
rechthoek zo klein mogelijk.
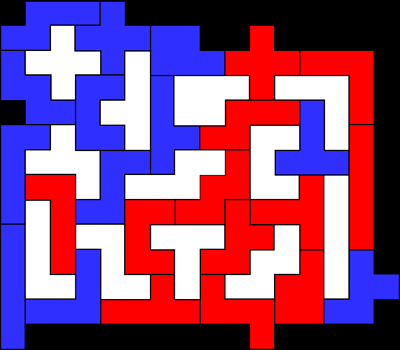
In ons voorbeeld is de omgesloten rechthoek 16 x 14
Een andere oplossing van Michael Keller zie je op
http://www.solitairelaboratory.com/pentmino.html.
Deze oplossing is in een rechthoek van 18 x 13. Het kan echter veel beter.
Pento-Product-Xudoku
Op aanvraag, omdat we weten dat we bezoekers hebben die van
sudoku houden maakte Aad van de Wetering voor ons deze mooie hintvrije opgave.
Martin Friedeman: "Wat een geweldige puzzelmaker is Aad toch!"
Matthijs Coster:" Ik doe met één van jouw prijsvragen mee. Op de
NWD
leerde ik dat het ging om een calcudoku, maar een lastige, en vooral
leuke. Nergens hoefde er te worden gegokt"
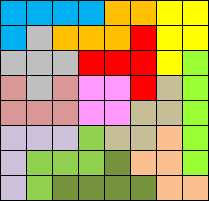
Zet de getallen van 1 tot 8 in elke rij, elke kolom en in de twee
diagonalen.
Je krijgt telkens het product van de getallen van elke pentomino.
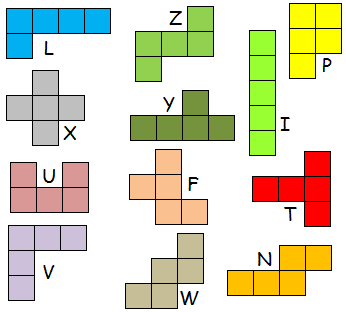
L:420, X:96, U:1080, V:11760, Z:576, Y:336, F:1440, W:84, P:720, I:1120,
T:384 , N:1680
Wil je graag een hint? Mail naar
o.d.m@fulladsl.be
Wie deze opgave leuk vindt, kan ook terecht op
www.321Monkey.nl
Opgave van Edo Timmermans
Omdat we Edo één van de creatiefste pentomino-fans is (zie
Pentomino
ansichtkaartenwedstrijd en
Het eiland van graaf
Penteviticole) vroegen we hem een opgave voor ons te maken.
Hij noemde de opgave:
"50.
Fifty-Fifty"
Zijn wedstrijd bestaat uit 2 delen.
Neem een rood 10x10-vierkant met een diagonaal groen vierkant
binnenin dat 50% van het oppervlak van het 10x10-vierkant bedekt.
De pentomino's dienen zodanig binnen het 10x10-vierkant geplaatst
worden, dat ze allemaal gedeeltelijk rood en gedeeltelijk groen zijn.
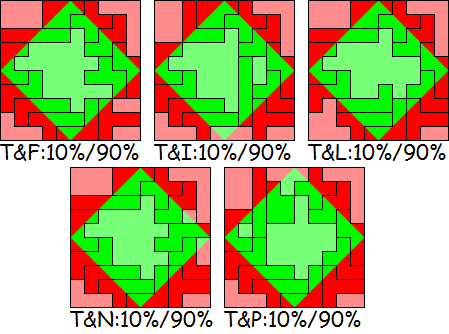
In de eerste 50% van de wedstrijd is het de bedoeling om
oplossingen te vinden waarin 10 pentomino's 50% rood en 50% groen zijn.
Tevens dienen alle pentomino's samen 50% rood en 50% groen te zijn. Aan
de voorbeelden is te zien dat dit niet zo moeilijk is, wanneer de
overige 2 pentomino's 10% rood of 10% groen mogen zijn. Daarom moeten
die 2 pentomino's minimaal 20% rood en minimaal 20% groen zijn, maar hoe
dichter bij 50% hoe beter natuurlijk.
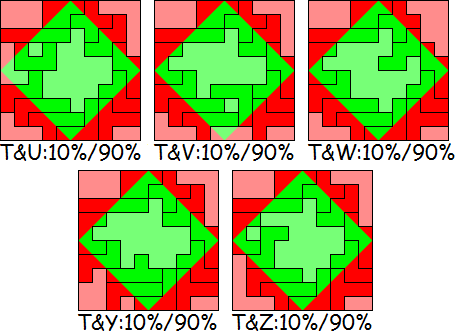
In de volgende 50% van de wedstrijd dien je symmetrische oplossingen te
zoeken. Er hoeven niet langer 10 pentomino's half rood en half groen te
zijn, maar er geldt nog steeds dat iedere pentomino gedeeltelijk rood en
gedeeltelijk groen moet zijn en dat alle pentomino's samen 50% rood en
50% groen moeten zijn.
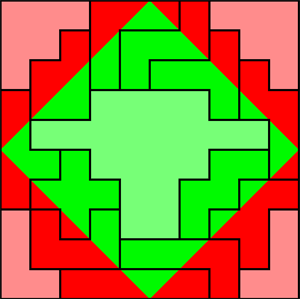
Het voorbeeld is geen goede oplossing omdat de W-pentomino volledig groen
is.
Computer programmeurs worden uitgenodigd om naar symmetrische
oplossingen te zoeken waarin tenminste 50% van de pentomino's 50% rood
en 50% groen zijn.
Pentorigami-opgave van Bob Henderson
Maak een pentominoset uit gekleurd papier.
We plaatsten per blad eenzelfde pentomino 6 maal zodat je dit kan gebruiken om op kleurpapier te fotokopiëren. Op die manier krijg je verschillende pentominosets.
F
I
L
N
P
T
U
V
W
X
Y
Z
Snij ook één van de vier rasterlijnen door die de P-pentomino snijden in
het centrum.
Er zijn acht pentomino's waarmee men een open doosje kan maken:
F,L,N,T,W,X,Y en Z
Voeg zes van deze doosjes samen. De figuur ziet eruit alsof er zes
kubussen staan op de zijvlakken van een zevende kubus die verborgen is
in het midden.
|
|
|
Neem nu I,P,U en V-pentomino (degene waarmee je
geen open doosje kan maken) samen met twee andere pentomino's en probeer
door te vouwen en samen te voegen dezelfde figuur te maken als hierboven
beschreven.
Je mag de pentomino's op verschillende manieren plooien.
3D-Opgave van Michael Dowle
Michael bedekt een kubus met een pentominoset.
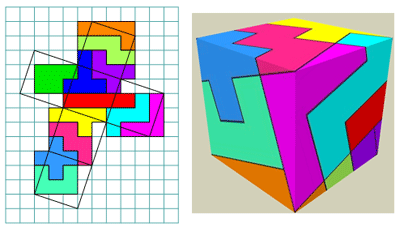
Al enkele jaren zijn er in
KSO Glorieux in het derde jaar leerlingen die voor hun werk
van Pythagoras een kubus bedekken.
http://www.pentomino.classy.be/versnijdenopkubus.html
Aad van de Wetering bedekt de kubus met dezelfde pentomino.
http://home.planet.nl/~avdw3b/kubuspoly.html
C. J. Bouwkamp schreef in 1998 reeds
een boek (dat we van hem gekregen hebben) "Tiling the surface of the
cube by 12 identical pentominoes"
Ook op de volgende sites vind je bedekkingen van een kubus.
http://www.ericharshbarger.org/pentominoes/article_06.html
http://www.tzingaro.com/artelectric/pentominoes06.html
http://home.educities.edu.tw/proteon/note131.htm
http://www.iread.it/lz/pag3_eng.html
Michael bedekt ook driehoekige dipiramides
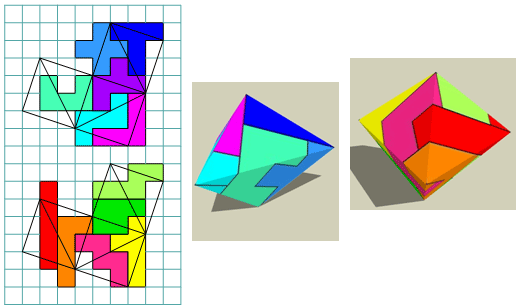
Dit hebben we nergens anders gevonden.
En dan nu zijn mooi opgave:
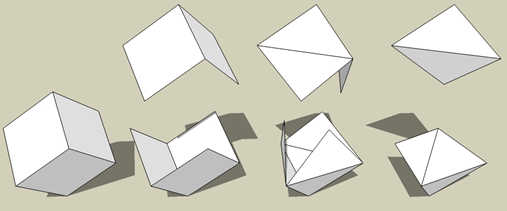
Vind een schikking met een pentominoset waarmee je een kubus kan
bedekken maar die je ook kan verdelen in twee helften die de bedekking
zijn van van driehoekige dipiramides.
Je mag de pentomino's niet herschikken.
Het probleem is voorgesteld in de tekening hieronder.
Pentomino's met een touwtje
Onze inspiratie komt uit het leuke boek "Denkwaar" van Jaap
Klauwen.
Dank aan Aad Thoen die ons dit boek toestuurde.
Veen Magazines schenkt een boek aan de
winnaar van deze opgave.

Voor de berekeningen gebruik je de stelling van Pythagoras.
We laten de hoekpunten van de pentomino's samenvallen met roosterpunten.
De maatgetal van de zijde van een vierkantje stellen we 1. Elke
pentomino moet minstens één zijde gemeenschappelijk hebben met een
andere.
We spannen een touwtje ronde de roosterpunten van de set pentomino's en
trekken het strak.
Plaats de pentomino's zodanig dat de omtrek maximaal is.
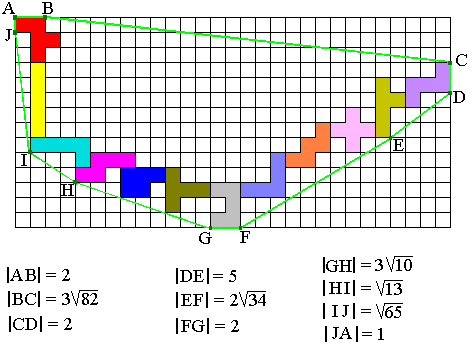
In het bovenstaande voorbeeld is de omtrek van het touw (groene lijn)
71.98
op 0,01 nauwkeurig.
Je moet dus een zo groot mogelijke omtrek hebben.
We hebben dit al eens besproken bij
pentomino-rechthoeken.
Opgave van
Alexandre Owen Muniz
Alexandre stuurde ons een mail met een wedstrijdprobleem maar we
begrepen het niet goed. We gingen te rade bij Helmut Postl en we kregen
van hem een heel mooie uitleg .
Bijvoorbeeld van de L-tetromino maken we de T-tetromino.

We kunnen de T-tetromino transformeren naar een volgende en zo verder. Op die manier kunnen we een tetromino-ketting bouwen.
Als in de ketting elke teromino juist één keer voorkomt en dat de begin- en eindtetromino dezelfde is, dan hebben we een cyclus gemaakt. In de cyclus is de starttetromino niet belangrijk aangezien een cyclus geen begin of einde heeft
In het volgende voorbeeld heeft elk vierkant van de tetromino zijn eigen kleur, zodat men beter de verplaatsing ziet.

Deze cyclus bevat de vijf tetromino's (L,N,Q,T,I) en we kunnen dat blijven herhalen.
Opmerking: de eind L heeft een andere inkleuring dan de begin L maar dat is van geen enkel belang.
In een cyclus moet de eind polyomino dezelfde oriëntatie hebben als de begin polyomino d.w.z. er mag niet gedraaid of gespiegeld worden maar er mag wel verschoven worden.
In het bovenstaande voorbeeld is de verschuiving de identieke permutatie. (nulvector). Als we de cyclus doorlopen blijven de tetromino's telkens op dezelfde plaats.
In het volgende voorbeeld
is de eind tetromino verplaatst over de vector (2,1):

Als we verder in de cyclus lopen zullen de polyomino's verder
wegschuiven.
De snelheid van de beweging wordt gemeten via de vector die bij
de verplaatsing van een polyomino binnen een cyclus hoort.
In het bovenstaande voorbeeld is dit (2,1).
De snelheid is de som van de absolute waarden van deze
coördinaatsgetallen, nl. 3. Deze manier van meten is natuurlijker dan de
Euclidische afstand (in dit geval de vierkantswortel uit 5) te nemen.
Alexandre noemt dit de 'taxicab distance' omdat het de afstand
neemt welke een taxi neemt wanneer hij de straat (roosterlijnen) volgt.
De snelheid van de cyclus in het eerste voorbeeld is nul.
Het wedstrijdprobleem:
Neem de 12 pentomino's en maak een cyclus waarbij de snelheid zo
groot mogelijk is.
Je mag dit zelfde probleem ook oplossen voor de hexomino's en eveneens
voor de eenzijdige pentomino's
Randopmerking: het
probleem doet denken aan
'Conway’s Game of Life'
Deze polyominocyclussen gelijken op de bewegingen van de zogenoemde 'glider'

De vector is (1,1)
Appendix
12 opgaven voor de 50-ste wedstrijd vonden we een mooi aantal maar van
George Sicherman kregen we een
puzzeltje dat perfect past voor 'Fifty
Puzzle'
Kies uit een set van 12 pentomino's, 2pentomino's zodanig dat je met de
overige 10 geen rechthoek met oppervlakte '50'
kan maken.
De oplossing is enig.
Opmerkingen van Helmut Postl: "You can even omit the '10x5'-condition
and ask for any rectangle since the 10x5 is the only possible one.
It would have been a nice '50'-puzzle since it equals the area of the
rectangle. And curiously enough, FP are the initials of 'Fifty Puzzle'".

