Oplossingen van de opgave van Aad Thoen : pentomino-eilandjes
Van Aad Thoen kregen we een oplossing van 110.
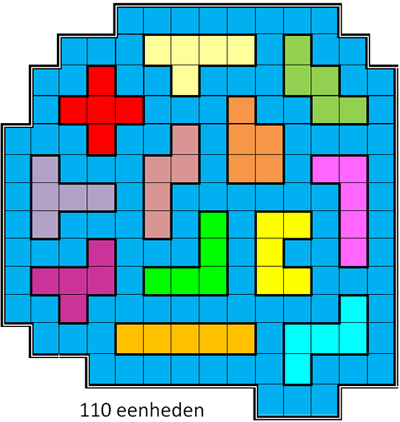
Dit resultaat kan met 1 eenheid verbeterd worden. Het bewijs gekregen van Frank Tinkelenberg en Helmut Postl vind je hieronder.
Records Wedstrijd 50
Oplossingen van de opgave van Aad Thoen : pentomino-eilandjes
Van Aad Thoen kregen we een oplossing van 110.

Dit resultaat kan met 1 eenheid verbeterd worden. Het bewijs gekregen van Frank
Tinkelenberg en Helmut Postl vind je hieronder.
Oplossing van Frank Tinkelenberg (109)
Hij mailde: "Ik kan beredeneren dat het minimum van blokjes water 108 moet
zijn; maar het is me niet gelukt die ook te vinden."
Omgeschreven rechthoek is 12x15

Hier volgt Frank zijn redenering dat 108 het theoretisch minimum is:
Teken rondom elke pentomino een waterrand ter grootte van een half blokje.
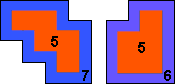
Oppervlak van blokjes + water blijkt 11 x 12 (5 pento + 7 water) + 11
van P-pentomino(5 pento + 6 water).
Dit water is verplicht om aan de regel te voldoen dat elke pentomino omringd
wordt door water.
Met deze omrande stukken kun je puzzelen net als met gewone pentomino's en het
resultaat is altijd een zee met pentomino's zoals bedoeld in de opgave.
Uiteraard is de waterrand aan de buitenkant dan te smal. Er moet aan alle kanten
nog een randje ter grootte van een half blokje bij. Het oppervlak van dat randje
is alleen afhankelijk van de grootte van de omgeschreven rechthoek.
Dit geldt ook als er in de hoeken openingen zijn, maar niet als er in de
zijkant nog openingen zijn, dan is er meer water nodig.
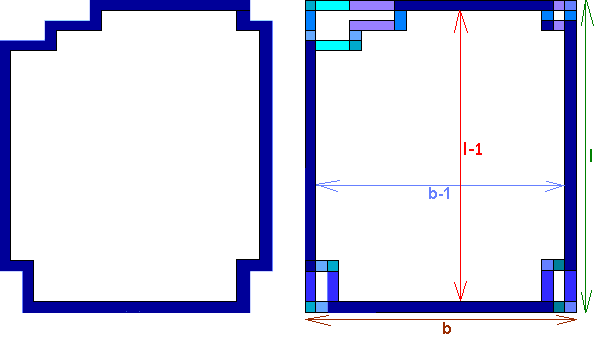
Oppervlakte van de waterrand= lb-(l-1)(b-1) = lb-(lb-b-l+1)=lb-lb+b+l-1=b+l-1
De totale wateroppervlakte kunnen we nu berekenen:
83 (rondom de pentomino's = 7 x 11 + 6) + breedte + lengte -1
We zoeken nu een rechthoek met zo klein mogelijke omtrek, maar groot genoeg om
alle omrande stukken te bevatten.
Ideale kandidaten blijken 12x14 of 13x13. Lengte + breedte = 26. Totale
wateroppervlak is 83 + 26 - 1 = 108.
De 12x14 is dan helemaal gevuld, de 13x13 houdt dan nog 1 vakje open,
waarschijnlijk in een hoek.
Frank: "Ik heb beide kandidaten uitgebreid geprobeerd, zonder een oplossing
te vinden. Ik zie echter ook geen reden waarom het onmogelijk is!
Let wel: mijn redenering zegt dat een oplossing met minder dan 108 niet kan
bestaan, maar niet dat 108 wel moet bestaan; het is prima mogelijk dat 109 wel
degelijk de beste oplossing is."
Helmut Postl: "I was able to prove that 109 is the minimum."
Toen we hiervoor meer uitleg vroegen mailde hij: "Yes, the proof is
correct. I did it also this way. Then I continued as follows:
Assume that there is a pattern with 108. Then, as stated correctly, the pattern
must be either a 12x14 rectangle or a 13x13 square with a hole. And this hole
must lie in a corner, otherwise the water perimeter (of width ½) is not of
shortest possible length. Now omit the water edge – this gives a 11x13 rectangle
resp. a 12x12 square with a corner hole – and try to fill in the extended
polyominoes of size 12 resp. 11 (for example, use Aad’s Flatpoly). You will soon
see that they will not fit. That’s it."
Wil je ons .fpo van de extended pentominoes, klik dan op het onderstaande
logo.

Opslaan en openen vanuit FlatPoly
Het schitterend programma “FlatPoly2” kun je
downloaden op de homepagina van Aad van de Wetering, Driebruggen.
http://home.wxs.nl/~avdw3b/aad.html
![]()
Opmerking: zijn de pentomino's en hun overeenkomstige uitbreidingen
gelijkvormige figuren?
We leggen het uit voor de P-pento
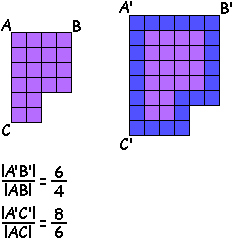
We zien dus dat de overeenkomstige zijden niet evenredig zijn !
Oplossingen van Bob Henderson: 109 eenheden
voor de zee
Bij vaststelling van fouten of onvolledigheid, mail
naar:
De omgeschreven rechthoek is telkens 13x14




Oplossing van Dario Uri (109)
Omgeschreven rechthoek 13x14

Oplossing van Aad van de Wetering (109)
Omgeschreven rechthoek 13x14
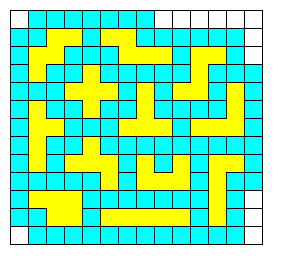
Oplossing van Helmut Postl (109)

Oplossingen van Peter Jeuken
Peter mailde: "Voor mijn oplossing van
het pentomino-eilandjes probleem ben ik uitgegaan van de 16x11
oplossing
van Tamme Afman bij
potpourri 11.
Door te schuiven met de pentomino's N, P en U kwam ik uit op een zee van 111
eenheden."

En dan kregen we een tweede oplossing:
" Mijn laptop heeft 6
dagen en 6 nachten onafgebroken gezocht naar de oplossing met 109 blauwe vakjes.
Vandaag stonden er ineens twee oplossingen op het scherm. De eerste staat
hieronder. De tweede is bijna gelijk. Alleen is de 'U' 180 graden gedraaid."

De tweede oplossing kan je hierboven vinden bij Helmut.
o.d.m@fulladsl.be