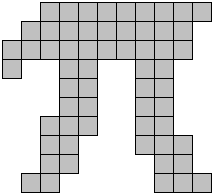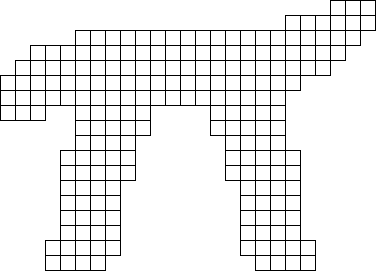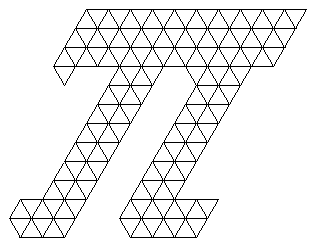Pi-dag met Pi-pento-puzzels

De datum 14 maart op z'n Amerikaans geschreven
lijkt erg op de eerste
decimalen van pi (het maatgetal van de oppervlakte van een cirkel met straal 1). Zo'n dag moet gevierd worden. Heel wat ideeën vind je op
http://glorieuxronse.classy.be/pi.html.
Pi-Pento-kalender
Op de Panama Conferentie werd ik aan de
Pentomino kalender herinnerd.
Deze is te koop bij
'Das Mathematikum'

Op de Pi-dag moet men natuurlijk het vakje 14 vrij laten.
Hierbij is FlatPoly van Aad van de Wetering een
enorme hulp.

In totaal zijn er
28 oplossingen
Bij L,P,U,V,Y, Z-combinatie is de oplossing
uniek!
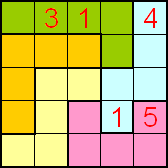
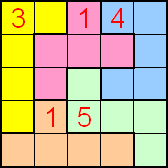
Pi-pento-puzzel
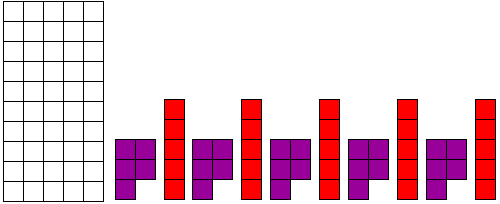
Ter gelegenheid van die dag tekenden we de letter 'PI'
met 60 vierkantjes en vulden hem met een pentominoset.

FlatPoly van Aad van de Wetering is hierbij een uitstekende hulp. (gratis te
downloaden op zijn homepagina)

Dit is onze puzzel.
Ga met de muisaanwijzer over de vorm en je ziet een oplossing.
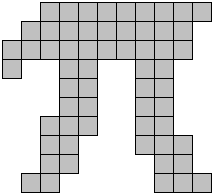
In de houtafdeling maakten ze met de CNC-machine onze
Pi-puzzel. Wie geen houtafdeling heeft kan hem ook in chocolade maken.

Voor de Pi-dag viering in
Viso te Mariakerke werd onze Pi-puzzel
gebruikt..

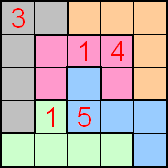
We maakten nog andere ontwerpen. Hieronder zie je er nog één.
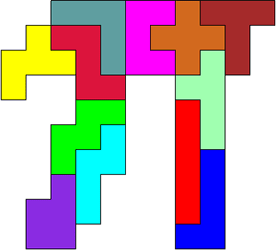
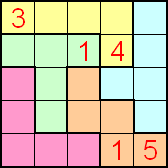
Ook Aad van de Wetering stuurde ons zijn Pi.
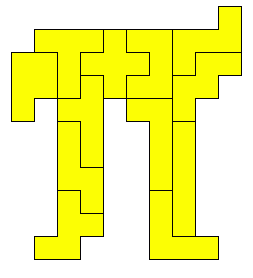
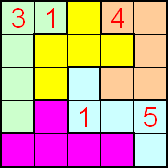
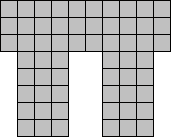
Van Peter Jeuken kregen we het volgende ontwerp.
We vinden het niet echt mooi maar ze is wel symmetrisch!
Ga met de muisaanwijzer over de vorm en je ziet een oplossing.
Van
Kate Jones kregen we op 14 maart 2011
volgende mail:"Here is a Pentomino Pi. I baked it just for you!"
Ga met de muisaanwijzer over de vorm en je ziet een oplossing.

Kan je het beter?
Edo Timmermans kon beter. Hij stuurde een hexomino-Pi. Hij dacht van van 210
(35x6) chocolaadjes te krijgen.
Ga met de muisaanwijzer over de vorm en je ziet een oplossing.
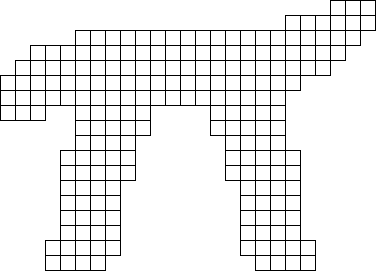
Voor de Pi-dag van 2024 stuurde Edo ons nog een (mooiere)
PI.
Ga met de muisaanwijzer over de vorm en je ziet een oplossing.

Mail een 'PI' naar
OdetteDM@outlook.com
Misschien belonen we wel met een chocolade 'PI'
Voor de Pi-dag 2017 maakten we de letter 'PI'
met 144 gelijkzijdige driehoekjes en vulden hem met twee sets hexiamonds en
wel zodanig dat dezelfde hexiamonds elkaar niet raken.
Hieronder zie je een set hexiamonds
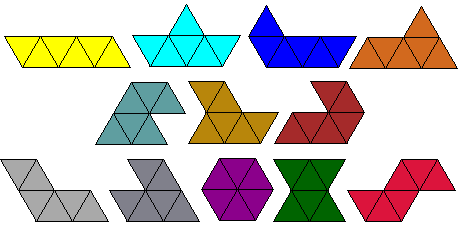
Polyamond van Aad van de Wetering is hierbij een uitstekende hulp. (gratis te
downloaden op zijn homepagina)

Dit is onze puzzel.
Ga met de muisaanwijzer over de vorm en je ziet een oplossing.
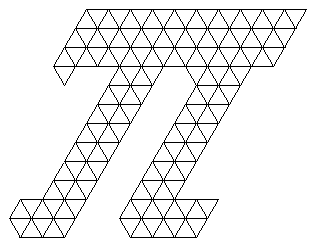
Pi X-Sudoku
In augustus 2016 kreeg ik een schitterend boekje
"Exotische sudoku's" van Aad Thoen en Aad van de Wetering.

Je kan het o.a. bestellen bij
Standaard Boekhandel.
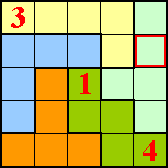
Op de kaft staat een leuke X-sudoku die we voor de duidelijkheid nog eens
hieronder plaatsen.
Er zijn geen pentomino's maar er moet flink nagedacht worden en hij is
uitstekend om de Pi-dag te vieren.
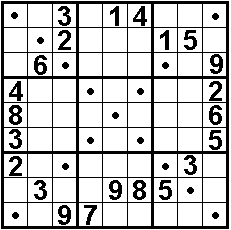
De stippen op de diagonalen betekenen dat de getallen op elke
diagonaal moeten verschillend zijn.
Tip: een kleine "9" lijkt op een komma
In het boekje vind je nog een PI-sudoku waarbij 15 cijfers van pi in
ruitvorm staan.
Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
| Aad Thoen |
Nederland |
| Aad van de Wetering |
Nederland |
| Odette De Meulemeester |
België |
| Sander Waalboer |
Nederland |
| Martin Friedeman |
Nederland |
| George Sicherman |
USA |
| Luc Gheysens en Ingrid Callens |
België |
| Ilse De Boeck |
België |
| Bob Henderson |
USA |
| Peter Jeuken |
Nederland |
| Nico Looije |
Nederland |
| Jolanda Nieuwhuis |
Nederland |
| Max Geven |
Nederland |
Jolanda Nieuwhuis won het boekje
"Exotische sudoku's" op de
NWD (Nationale Wiskunde Dagen) en dit was
haar reactie: "We zijn hier thuis allemaal al druk aan het puzzelen
geslagen. Leuke sudoku's!"
George Sicherman:"I found this
considerably harder to solve than
the Valentine's Day puzzle."
Bob Henderson: "These are great puzzles, but I am too lazy to solve
them myself, now that I have taught my computer how to solve them!"
Pi-Sudoku
In november 2019 kreeg ik van Aad van de Wetering de
volgende sudoku:
Pi met 20 decimalen in een "cirkel"
Laatste decimaal (6) is het middelpunt "cirkel"
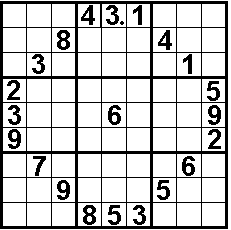
Diagonale buren zijn ongelijk
Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
| Aad Thoen |
Nederland |
| Aad van de Wetering |
Nederland |
| Odette De Meulemeester |
België |
| Martin van de Wetering |
Nederland |
| Matthijs Coster |
Nederland |
| Sander Waalboer |
Nederland |
| Martin Friedeman |
Nederland |
| Nico Looije |
Nederland |
| Peter Jeuken |
Nederland |
| George Sicherman |
USA |
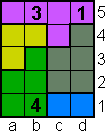
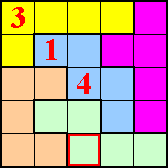
Pi-Tectonic
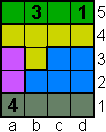
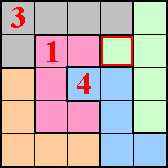
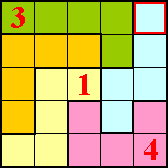
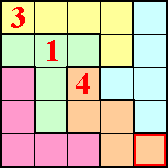
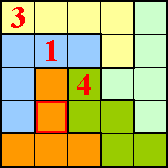
Vul de polyomino's met de cijfers 1,2,3, ... net zoveel als er vakjes zijn.
Vul 1 in bij een monomino, 1 en 2 bij een domino, ... 1,2,3,4 en 5 bij een
pentomino.
Vakjes met gelijke cijfers mogen elkaar niet raken ook niet bij de
hoekpunten.
De oplossing (met de redenering) krijg
je als je op de opgave of op de tekening drukt.
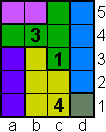
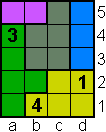
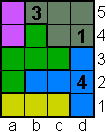
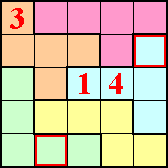
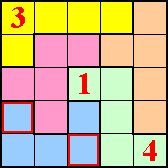
Bij de volgende pi-tectonics kan je met de muisaanwijzer over de tectonic gaan en je ziet de oplossing.
|
Opgave 6
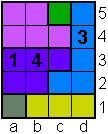 |
Opgave 7
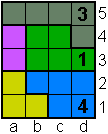 |
Opgave 8
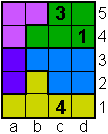 |
Opgave 9
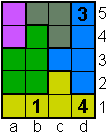 |
Opgave 10
 |
|
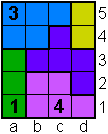
Opgave 11
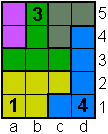 |
Opgave 12
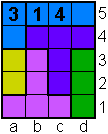
3 is overbodig. |
Opgave 13
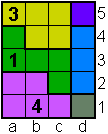 |
Opgave 14
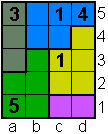 |
Opgave 15
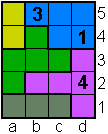
3 is overbodig. |
|
Opgave 16
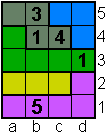 |
Opgave17
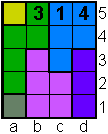
1 is overbodig. |
Opgave 18
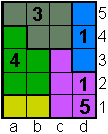
1 op d4 en 5 op d1
zijn overbodig |
Opgave 19
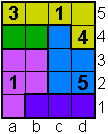 |
Opgave 20
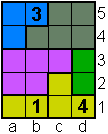 |
|
Opgave 21
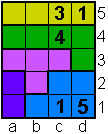
3 op c5 en 1 op c1
hoeft niet. |
Opgave 22
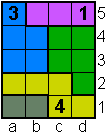 |
Opgave 23
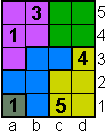 |
Opgave 24
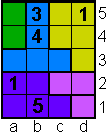
1 op a2 en 3 op b5
zijn overbodig. |
Opgave 25
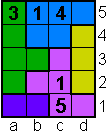
1 op b5 en 5 op c1
zijn overbodig. |
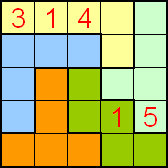
Pi-Tectonic
van Matthijs
Vul de pentomino's met de cijfers 1,2,3, 4 en 5.
Vakjes met gelijke cijfers mogen elkaar niet raken ook niet bij de
hoekpunten.
Daarnaast dienen in elke rij driemaal de getallen 1 tot en met 5 te worden
geplaatst en in elke kolom éénmaal.
Matthijs gaf nog een aanvullende hint: als je ergens een kolom met de
getallen 1 t/m 5 hebt gevonden, dan zijn er maar een zeer beperkt aantal
mogelijkheden voor de belendende kolommen.
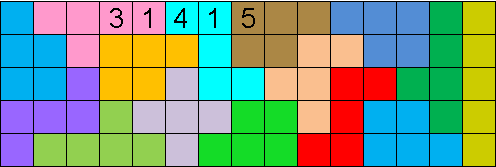
Wil je een opgave zonder kleur om af te drukken?
Hier duwen.
Goede oplossers verwerven eeuwige roem.
Mail je oplossing naar:
o.d.m@fulladsl.be
| Naam |
Land |
| Matthijs Coster |
Nederland |
| Aad van de Wetering |
Nederland |
| Odette De Meulemeester |
België |
| Nico Looije |
Nederland |
| Martin Friedeman |
Nederland |
| George Sicherman |
USA |
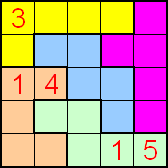
Pi-Sutecs
van Matthijs
Voor onze workshop
P(Q)RS 5 op NWD 25 maakte Matthijs deze
Pi-Sutec.
Meer ideeën om de PI-dag te vieren kan je vinden in onze
syllabus
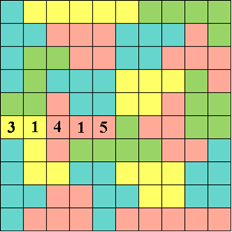
In elke rij en kolom moeten tweemaal de getallen 1 t/m 5 worden geplaatst,
zodat in elke pentomino de getallen 1 t/m 5 staan en zo dat nergens 2
dezelfde getallen naast elkaar staan, niet boven elkaar, niet naast elkaar
en niet diagonaalsgewijs.
Goede oplossers verwerven eeuwige roem.
Mail je oplossing naar:
o.d.m@fulladsl.be
| Naam |
Land |
| Matthijs Coster |
Nederland |
| Odette De Meulemeester |
België |
| Nico Looije |
Nederland |
| Martin Friedeman |
Nederland |
| George Sicherman |
USA |
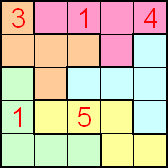
Matthijs maakte er nog eentje
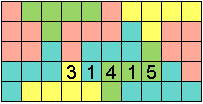
In elke rij moeten tweemaal de getallen 1 t/m 5 worden geplaatst en in elke
kolom juist éénmaal zodat in elke pentomino de getallen 1 t/m 5 staan en zo dat nergens 2
dezelfde getallen naast elkaar staan, niet boven elkaar, niet naast elkaar
en niet diagonaalsgewijs.
Goede oplossers verwerven eeuwige roem.
Mail je oplossing naar:
o.d.m@fulladsl.be
| Naam |
Land |
| Matthijs Coster |
Nederland |
| Odette De Meulemeester |
België |
| Nico Looije |
Nederland |
| Martin Friedeman |
Nederland |
| Gert-Jan Stockman |
België |
| Sofie Rijckaert |
België |
| Tine Verplancke |
België |
| Sofie Mailliard |
België |
| Ilse De Boeck |
België |
| Aad van de Wetering |
Nederland |
| Yana Vander Rasieren |
België |
| Lieven Van Rijckeghem |
België |
| Roel Huisman |
Portugal
|
| Aad Thoen |
Nederland |
| George Sicherman |
USA |
| Berend Jan van der Zwaag |
Nederland |
| Luc Gheysens |
België |
| Matthias Maes |
België |
| Jeanne Monstrey |
België |
| Eleonore Ovyn |
België |
| Mattis Saint Germain |
België |
| Peter Hendriks |
Nederland |
| Cindy Baert |
België |
| Sylvie De Smet |
België |
| Sofie Vermeersch |
België |
Berend Jan :"Een fijn pipuzzeltje!"
5x5
Pi-Pento-SudokuWe kozen voor een 5x5 bord gevuld met
vijf verschillende pentomino's. Als we de I- en P-pentomino uitsluiten dan
zijn er nog zeven verschillende mogelijkheden om dit bord te leggen.
Deze opgave maakte Aad van de Wetering voor ons op
aanvraag.
Plaats in elke rij, in elke kolom en binnen elke pentomino de cijfers
1,2,3,4 en 5.
Ga met de muisaanwijzer over de vorm en je ziet een oplossing. (Eerst zelf
oplossen!)

De rest maakten we zelf. Als je er ook één maakt die we mogen plaatsen mail
dan naar
o.d.m@fulladsl.be
Op de 'open school' waren de pi-pento-sudoku een succes.
Wil je nog meer pento-sudoku? Kijk dan op
http://pentomino.classy.be/sudoku.html
Wil je het voorgaande in een document zonder kleur? Je
kan het
hier downloaden.
Tine Verplancke (Prizma
Middenschool - Izegem) en haar leerlingen van 1B hielden een projectdag en hadden 4 opdrachten gebruikt (mits wat aanpassing en/of extra
duiding) uit onze workshop.
"De escape room was een erg succes bij de leerlingen én voor mij ook
aangezien ze 60 minuten met wiskunde zijn bezig geweest"

Omdat eenvoud aantrekt wilden we opgaven maken met 3,14
maar dan kan men natuurlijk 2 en 5 van plaats wisselen.
Toen we op
www.nksudoku.nl de evensudoku zagen ontstond het idee van de
onderstaande opgaven die Aad van de Wetering voor ons maakte.
Plaats in elke rij, in elke kolom en binnen elke pentomino de cijfers
1,2,3,4 en 5.
In een rood omrand vakje moet altijd een even getal staan.
Wil je het voorgaande in een document zonder kleur? Je
kan het
hier downloaden.
Aads
Pi-Mono-Tetro-Pento-Sudoku
Aad van de Wetering maakte voor ons deze moeilijke Pi-tetro-pento-sudoku.
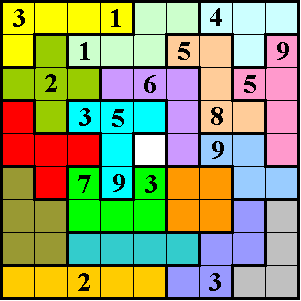
In elke kolom en op elke rij moet men de cijfers van 1 t/m 9 komen.
De som van de cijfers in een pentomino moet 25 zijn (hoeven niet
verschillend te zijn).
De som van de cijfers in een tetromino moet 20 zijn.(Ze hoeven niet
verschillende te zijn).
Omdat we onmiddellijk het middelste vakje vonden door te berekenen en ook
het centrale vak van de Z-pento dachten dat het oplossen nogal vlot ging
gaan, maar dan...
Wil je de vierde rij als hint?

Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
Hint |
| Aad van de Wetering |
Nederland |
- |
| Odette De Meulemeester |
België |
x |
| Sander Waalboer |
Nederland |
- |
| Lisan Sanders |
Nederland |
- |
| Peter Jeuken |
Nederland |
x |
| Martin Friedeman |
Nederland |
- |
| Bert ten Hoeve |
Nederland |
- |
| Berend Jan van der Zwaag |
Nederland |
- |
| Bob Henderson |
USA |
- |
| Helmut Postl |
Oostenrijk |
- |
tr>
Nico Looije |
Nederland |
- |
Odette deed er meer dan een dag over
terwijl Sander zijn computer het deed in 40 seconden!
Lisan mailde:"De tijd die ik eraan besteed heb, weet ik niet precies
meer, maar heel wat uurtjes. Wel heel leuk om te doen!
Bedankt voor dit moois en voor sudoku’s houd ik me altijd aanbevolen."
Peter Jeuken:"Ik ben met hetzelfde computerprogramma aan de gang gegaan
waarmee ik wedstrijd 42
heb opgelost. Maar al snel bleek dat het programma in dit geval te traag
was. Daarom heb ik toch maar van de hint gebruik gemaakt. Toen kwam de
oplossing in ongeveer 1 minuut."
Martin Friedeman:"Aad weet ze maar mooi te verzinnen! Op
zijn thuispagina zijn ook al van die
exotische creaties te bewonderen. Maar goed, deze
‘Pi-Mono-Tetro-Pento-Sudoku’ heeft behoorlijk wat vrije tijd gekost. Niet
dat ik dat erg vind hoor, ’t houdt me immers van de straat én van de fles!
;-)"
Bert ten Hoeve:"Ik ben net terug van
vakantie en heb me meteen maar op de puzzel van Aad geworpen. Inderdaad, erg
lastig, maar zie hier het resultaat (uiteraard zonder hint). Nogmaals mijn
dank, ook aan Aad en hartelijke groet"
We kregen van Berend Jan de oplossing van wedstrijd 45 binnen en hij
mailde:"Zo'n sudoku is altijd leuk in de vakantie.En omdat ik toch al
lekker bezig was heb ik Aads Pi-Mono-Tetro-Pento-Sudoku er meteen maar
achteraan geplakt. Die was trouwens wel een stuk lastiger..."
Bob Henderson mailde:"Here is my solution to Aad's
Pi-Mono-Tetro-Pento-Sudoku puzzle. I did not look at the extra clue. My
Excel solver did not work for this puzzle, so I revised my other Sudoku
solver program (written in C and compiled to run on my Windows PC). It took
me an hour to get it to work properly, but then it solved the puzzle in less
than 1 second!"
Helmut Postl:"I remember that I started to solve it and I got many cases
to check. Then I wanted to program the computer, and the program did not get
finish. But now I got it.
Beautiful, pi to 18 decimals! Incidentally the same number as polyominoes
used (12 pentos, 5 tetros and 1 mono)."
Nico Looije:"ik
probeer ze in eerste instantie handmatig op te lossen maar dat lukt meestal
niet (binnen mijn geduldslimiet),dus deze sudoku’s heb ik met hetzelfde
programma opgelost c.q. gecontroleerd (allemaal in minder dan 8-honderdste
seconde)
Dank je wel ook voor de immer creatieve Aad"
Bob Henderson maakte voor ons ook een Pi-Poly-Sudoku-puzzel
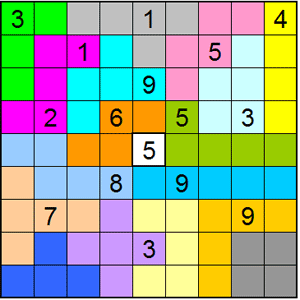
De gegeven getallen zijn de 3 en de decimalen van PI
Merk op dat de gegeven getallen symmetrisch staan.
In elke kolom en op elke rij moet men de cijfers van 1 t/m 9 komen.
De som van de cijfers in een pentomino moet 25 zijn (hoeven niet
verschillend te zijn).
De som van de cijfers in een tetromino moet 20 zijn.(Ze hoeven niet
verschillende te zijn).
Wil je drie getallen meer gegeven, druk dan op hint

Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
Hint |
| Aad van de Wetering |
Nederland |
- |
| Peter Jeuken |
Nederland |
x |
| Helmut Postl |
Oostenrijk |
- |
| Bert ten Hoeve |
Nederland |
x |
| Lisan Sanders |
Nederland |
x |
| Martin Friedeman |
Nederland |
- |
| Sander Waalboer |
Nederland |
- |
| Nico Looije |
Nederland |
- |
Aad van de
Wetering:"Mijn solver geeft één oplossing. Maar zegt er meteen bij dat ie
niet beredeneerbaar is, er moet meer dat tien keer gegokt worden. De
pi-hints staan wel erg mooi symmetrisch!"
Peter Jeuken:"Het is me met enige moeite gelukt om de
pi-poly-sudoku-puzzel van Bob Henderson op te lossen. Mijn solver was
aanvankelijk veel te traag om de oplossing binnen een redelijke tijd te
vinden. Na enkele verbeteringen vind ik hem eigenlijk nog niet snel genoeg.
Daardoor heb ik wel van de hint gebruik moeten maken."
Helmut Postl:"Bob’s pi-sudoku is just as beautiful as Aad’s. It shows
two decimals less, but it has a nice symmetry. Great! I tried to solve it by
hand, but I failed just like with Aad’s, there’s so many cases to check. So
I did it again by computer."
Bert ten Hoeve: "De eerste opgave is inderdaad een stuk lastiger dan
de andere twee, maar het is me toch gelukt zonder te programmeren. Eerst
zoveel mogelijk berekenen/beredeneren, dan de hints toevoegen en zie daar,
met wat geluk ....."
Lisan Sanders:"Nr. 1 vond ik de moeilijkste, ik heb uiteindelijk wel
de hints moeten gebruiken"
Martin Friedeman:"Na enorm veel geploeter heb ik Bobs monster – want
dat is het! – weten te verslaan. Ik ga daar zo een straffe Duvel op
drinken."
Onderaan de oplossing van Nico Looije stond dit:

Het betekent dat hij 1 oplossing gevonden heeft in 16 milliseconden
Bob stuurde ons een makkelijker toe
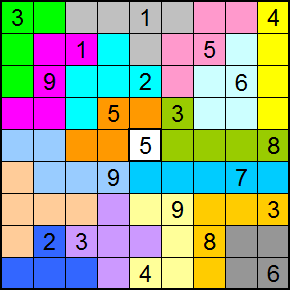
In elke kolom en op elke rij moet men de cijfers van 1 t/m 9 komen.
De som van de cijfers in een pentomino moet 25 zijn (hoeven niet
verschillend te zijn).
De som van de cijfers in een tetromino moet 20 zijn.(Ze hoeven niet
verschillende te zijn).
Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
| Peter Jeuken |
Nederland |
| Aad van de Wetering |
Nederland |
| Helmut Postl |
Oostenrijk |
| Bert ten Hoeve |
Nederland |
| Martin Friedeman |
Nederland |
| Lisan Sanders |
Nederland |
| Sander Waalboer |
Nederland |
| Nico Looije |
Nederland |
Peter Jeuken:
"Deze
puzzel is met 21 startcijfers een stuk gemakkelijker. Ondertussen heb ik
mijn programma een stuk sneller gemaakt. De computer deed er 8 seconden over
om de volgende oplossing te vinden."
Aad van de Wetering:"Ja, mooi allemaal!
Mijn solver beweert nog steeds dat ze niet zonder gegok oplosbaar zijn. In
de laatste kun je in kolom 8 3 cijfers beredeneren. Maar dan…"
Helmut Postl: "Bob’s new sudoku was really easier, this time I could
do it by hand. Fine!"
Bert ten Hoeve: "Verslavende puzzels ! Qua niveau, oplosbaarheid en
puzzelplezier is deze 2e helemaal vergelijkbaar met de 3e puzzel ! Heerlijk,
bedankt en hartelijke groet."
Martin Friedeman:"Wat een heerlijke puzzel! Bedankt voor het plaatsen
ervan, en Bob bedankt voor de verpozing!"
Lisan Sanders:"Nr. 2 was zoals aangekondigd een stuk makkelijker "
Onderaan de oplossing van Nico Looije stond dit:

Het betekent dat hij 1 oplossing gevonden heeft in 93 milliseconden.
Bob is wel heel ijverig
Hij maakte nog een Pi-poly -sudoku maar nu één van 10x10
In elke kolom en op elke rij moet men de cijfers van 1 t/m 10 komen.
De som van de cijfers in een pentomino (hij gebruikte juist een set) en in
een tetromino (waarvan er 2 sets zijn) moet 25 zijn (hoeven niet
verschillend te zijn).
Bob: "You should be able to solve this puzzle manually if you are as
patient as I was. . ."
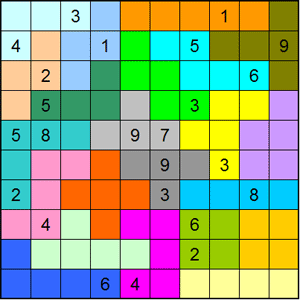
We vonden 2 getallen op de eerste rij maar dan...
Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
| Aad van de Wetering |
Nederland |
| Peter Jeuken |
Nederland |
| Martin Friedeman |
Nederland |
| Helmut Postl |
Oostenrijk |
| Bert ten Hoeve |
Nederland |
| Lisan Sanders |
Nederland |
| Sander Waalboer |
Nederland |
| Nico Looije |
Nederland |
Aad van de Wetering:"Mooie
opgave, maar niet gokvrij."
Peter Jeuken:"Dit keer een 10x10 sudoku! Met veel plezier heb ik de
computer aan het werk gezet."
Helmut Postl:"Bob’s ideas are great! I am proud to have had the
patience for solving the 10x10 by hand, just as Bob did"
Bert ten Hoeve:"Prachtige opgave, niet direct makkelijk maar wel
helemaal met de hand en het hoofd te beredeneren / berekenen.
Zeer bedankt, ook Bob natuurlijk, en hartelijke groet"
Martin Friedeman:"Gisteravond, tijdens Kameroen – Denemarken, heb ik
Bobs derde Pi-Poly-Sudoku-Puzzel weten te kraken. Deze is inderdaad compleet
‘met de hand’ te doen."
Lisan Sanders:"Bij nr.3 heb ik veel moeten gokken op plaatsen waar
nog maar 2 cijfers mogelijk waren. Wat een kick als het dan uiteindelijk
lukt. Heel hartelijk bedankt, ook Bob voor zoveel moois. Ik heb me er
kostelijk mee geamuseerd."
Sander Waalboer:"De afgelopen jaren heb ik onder meer een
eigen sudoku-solver gebouwd en doorontwikkeld.
Het oplossen van de meeste sudoku’s (zoals jouw huidige) is volledig
standaard functionaliteit.
Daar hoef is dus (helaas) niets voor te programmeren…."
Nico Looije vond deze oplossing (zijn computer ;-) in 15
milliseconden.
Andere PI-sudoku's staan op:
http://glorieuxronse.classy.be/pipuzzels.html
Pentomino-Slinger
14 maart 2011
'PI' maken met twee
pentominoslingers.

Wie wint het?
Thijs is overmoedig: hij probeert het met een hexominoslinger.

Van Edo Timmermans kregen we naar aanleiding van George Sicherman zijn
PI-pentoe een 5PI-puzzel: het is mogelijk
om in een 5x10-rechthoek 5 P-pentomino's en 5 I-pentomino's te plaatsen,
zodanig dat er 5 niet-overlappende gebiedjes zijn die elk één I- en één
P-pentomino bevatten, die met elkaar verbonden zijn.
Wil je de oplossing zien? Klik op de opgave.