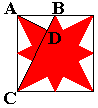
Welk percentage van de Z-pentomino is rood gekleurd?
De stervormige figuur is verkregen door in een vierkant elk midden van een
zijde te verbinden met de hoekpunten van de overstaande zijde.

We vonden de inspiratie voor deze vraag bij de Vlaamse Wiskunde Olympiade 1991-Eerste ronde.
Welk percentage van de Z-pentomino is rood gekleurd?
De stervormige figuur is verkregen door in een vierkant elk midden van een
zijde te verbinden met de hoekpunten van de overstaande zijde.

Oplossing
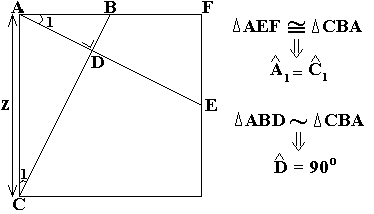
Als we weten dat rechten loodrecht op elkaar staan
als het product van hun richtingscoëfficienten gelijk is aan -1 dan hebben we
het voorgaande niet nodig voor dit bewijs.
We kunnen de lengte van [ BC ] berekenen met de stelling van Pythagoras.
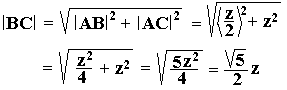
De lengten van [ BD ] en [ AD ]
berekenen we met de evenredigheid van zijden van de gelijkvormige driehoeken.
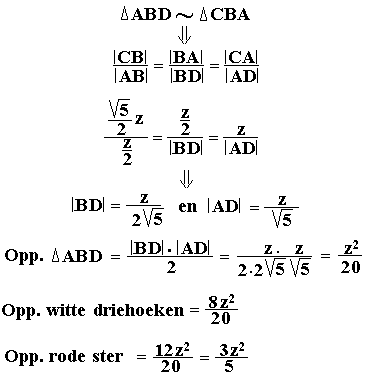
Dit betekent dat 60% van de Z-pentomino rood gekleurd is.