Records Wedstrijd 42
 |
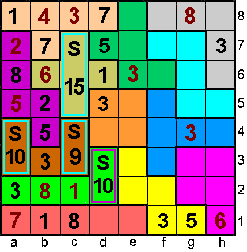
1+2+3+4+5+6+7+8=36=>de som van de
getallen van elke rij en elke kolom is 36.
In I-pento is de som 22=> op rij 1 hebben we reeds 28 dus is f1 + g1 =
8.
7+1 en 6+2 kan niet, dus kan alleen 3 en 5 en moet 3 op f1 en dus 5 op
g1
Op a6 kan 1,4 of 8
Als we 1 plaatsen op a6 moet in N-pento (som 22) b5+b4=14=7+7=6+8 en dat
kan niet.
Als we 4 plaatsen op a6 moet in N-pento b5+b4=11=3+8=4+7=5+6 en dat kan
niet.
Op a6 moet dus 8=>b5+b4=7=1+6=3+4=2+5
Het enige dat kan is 2 en 5=> op b5 moet 2 en op b4 moet 5
Op b1 kan alleen nog 1 (verticaal en horizontaal kijken) |
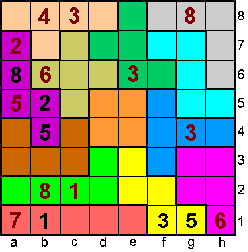 |
Op b7 kan alleen 3 of 7.
Stel 3 dan hebben we reeds in de Y-pento een som van 10 dus moet
a8+d8=12=6+6=5+7 en geen van beide kan.=>b7 is 7 en dan moet 3 op b3.
In kolom a kan 3 dan alleen op plaats b2. |
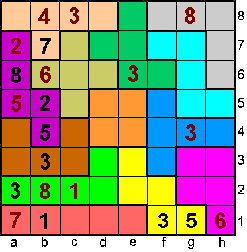 |
Op a8 is het 1 of 6.
Stel dat het 6 is dan is a4+a3=5 en is c3+c4=14. (som U-pento=22). Die
som kan alleen 6+8 zijn=>
c1 is 2 of 4
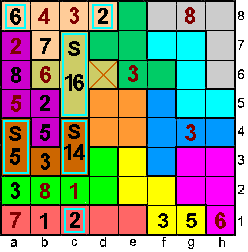
c1=2=>c5+c6+c7=16
Kan niet want in de X-pento
blijft dan 0 voor d6 |
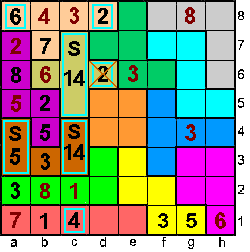
c1=4=>c5+c6+c7=14
Kan niet want op c4 moet dan 2
(som X-pento is 22) |
Op a8 komt dus 1 en dan is 7 op d8 omwille
van een som van 22 in Y-pento |
Op c1 komt 2,4 of 8
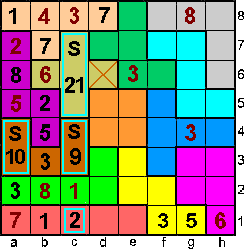
Stel op c1=2. Dan is c5+c6+c7=21 maar dit kan
niet want de som in X-pento is 22 |
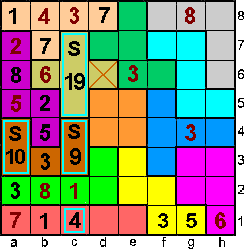
Stel op c1=4. Dan is c5+c6+c7=19 maar dit kan niet want de som in
X-pento is 22 |
|
| =>Op c1 staat 8 |
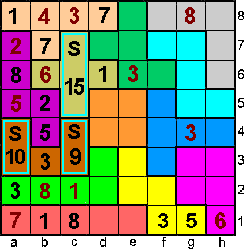 |
c5+c6+c7=15
In de X-pento is de som 22 dus moet 1 op d6
In de L-pento is de som 22 dus is d2+d3 = 10 => 5 kan niet op d2 en ook
niet op d3.
In kolom c kan 5 enkel op d7 en dan kan 3 alleen op d5 en moet h7 ook 3
zijn. |
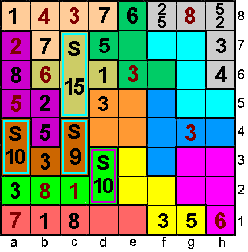 |
6 moet dus op e8 en op h6 moet 4.
In de F-pentomino is de som 22 => e7+f6=8
8=1+7=2+6=3+5=4+4
Het enige dat kan is 1 op e7 en 7 op f6
|
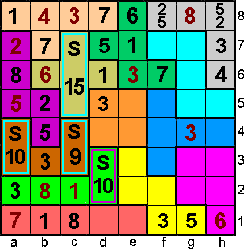 |
Rij 6: 5 kan alleen op c6 en dus 2
op g6.
Rij 7: 8 kan alleen op f7 |
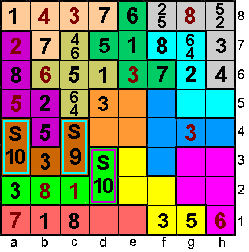 |
Op g7 staat 6 of 4
Stel g7 is 6 dan is g5+h5=22-16=6 (omwille van de som 22 in Z-pento)
6=1+5=2+4=3+3. Geen enkele combinatie kan =>g7 is 4 en dan staat 6 op c7
Op c5 staat dan 4. |
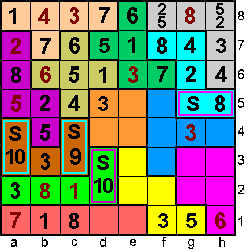 |
g5+h5=8
(omwille van de som 22 in Z-pento)
8=1+7=2+6=3+5
Het enige dat kan is 1 en 7=>e5 is 8 en f5 is 6 |
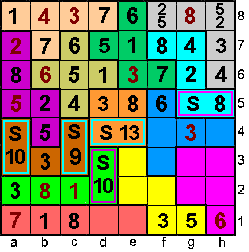 |
Elke rij heeft 36 als som:
1+2+3+4+5+6+7+8.
Er zijn 8 rijen dus is de totale som 8 x 36 = 288.
De som van alle getallen in de pentomino's is 12 x 22 = 264.
De som van de getallen in de
tetromino (vierkant) is 288 - 264 = 24.
De som van d4 en e4 is 13=6+7 => d4=6 en e4=7.
Op a4 moet 4 staan en op a3 staat 6.
Op c3 moet 7 staan en op c4 staat 2. |
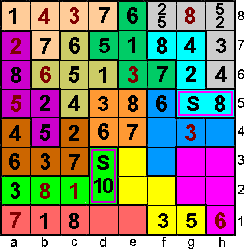 |
d2+d3=10=2+8=3+7=4+6=5+5
Het enige dat kan is op d3 een 8 plaatsen en d2 staat dan 2.
Op d1 moet dan volgens kolom d een 4 staan en volgens rij 1 moet op e1
een 2
Op rij 4 moet op h4 een 8, dus staat 1 op f4 |
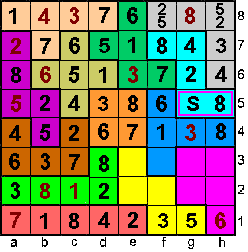 |
In de T-pento is de som 22 dus op
f3 staat 22-(1+3+8+6)=4.
Op f2 komt dus 5 en op f8 staat 2 en dus op h8 staat 5. |
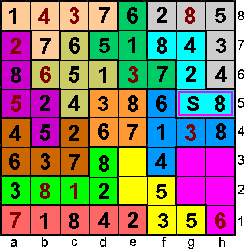 |
Op e3 moet een 5 en op e2 staat 4.
Op h3 moet 2 en op g3 moet 1 |
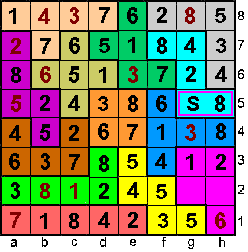 |
Op g2 staat 6 en op h2 staat 7.
Op h5 staat 1 en op g5 staat 7. |
Dus de oplossing:

In de lijst vind je de namen van degenen die ons een juiste oplossing stuurden.
Als je op de naam klikt zie je hun oplossing.
Onder de naamlijst vind je de commentaren die ze ons toestuurden.
Martin Friedeman:"Deze puzzel lijkt me inderdaad
makkelijker dan die
eilandpuzzel.
Wat een heerlijke opgave, en inderdaad: élk cijfer is beredeneerbaar! Groeten,
en graag tot een volgende keer!"
Sander Waalboer:"Sudoku's die te beredeneren zijn vind ik doorgaans
wel leuk. Omdat er nergens staat dat de getallen per pentomino uniek moeten zijn
vraag ik me af de oplossing die in de bijlage bij dit mailtje staat goed kan
zijn. Ik hoor het wel van je...
Dank in ieder geval voor de puzzel."
Lisan Sanders:"Leuk dat je mij deze Sudoku stuurde. Ik had net vorige week de laatste
Ukodus+ van Aads site opgelost en me eigenlijk voorgenomen voorlopig
sudoku’s maar voor gezien te houden. Maar deze zou helemaal beredeneerbaar zijn
en dat sprak me toch wel aan. Ik begon wel eerst helemaal verkeerd, omdat je bij
Aad geen dezelfde cijfers in een pentomino mocht zetten en ik vond het best
moeilijk om eraan te wennen dat het hier wel mocht, moest zelfs. Ik begon met
uit te rekenen dat er in de 4 centrale vakjes een som van 24 moest komen en
vraag me nu niet naar de volgorde, maar het liep al gauw als een trein, vooral
doordat je veel paartjes kon maken.
Dus hartelijk bedankt hiervoor.
Lisan, die gek is op Belgische chocolade."
Sander Waalboer en Lisan Sanders verwierven ook eeuwige roem met onze 'Aads
Pi-Mono-Tetro-Pento-Sudoku'.
Proficiat!
Annelies Vanneste:"Na veel zoeken heb
ik de oplossing van de sudoku gevonden, met dank aan mijn broer die me de tip
gaf de som van de cijfers van het middelste vierkantje te berekenen."
Bert ten Hoeve:"Dit is geheel in mijn
straatje. Mooie puzzel, zo ben ik ze van Aad gewend, heerlijk. Ik heb de
oplossing stapsgewijze op de bijlage gezet, een hoop werk om het na te kijken.
Mocht hier iets op volgen dan kies ik voor de chocola !"
Bert is onze winnaar niet maar toch willen we hem belonen voor zo'n mooie uitleg
met chocolade.
Bob Henderson:"The attached Excel file contains my solution
to your pentomino sudoku puzzle. You should also be able to click on "Solve" to
run the solver macro (sorry, it takes a long time to run, but you can use the
"escape" key to stop it). The solver macro source code can be viewed using the
Visual Basic for Applications editor under tools -> Macro... -> Macros -> Sudoku
(select "edit" to view macro)."
Fer van Nieuwenhuizen:"Had ik niet al
eens gezegd dat de 13e m'n geluksdag is? Dat is dus wéér uitgekomen! Want ik heb
nét voor de vakantie je wedstrijdopgave opgelost! Ik kan de 13e dus onbezorgd op
vakantie. Nu hoop ik alleen maar, dat je de beschikking hebt over Excel. (Ik
gebruik Exel2003), want daarin heb ik mijn beredenering opgenomen. Ik heb Excel
niet gebruikt om een oplossing te vinden, maar het kopiëren van een diagram gaat
wat makkelijker. Want ik ben lui! De enige Excel-functie die ik heb gebruikt
zijn de kolom naast en de rij onder het diagram. Daarmee wordt bepaald welke
cijfers in de betreffende Rij/Kolom nog ontbreken. Met je hint over de fout in
C5 en C7 en een aanname mijnerzijds m.b.t. B1 en B3 (zie pag. 7 van het
Afdrukvoorbeeld) maak ik een afdruk voor
Alissa. Heb haar al over het "probleem" verteld
en ik ze begon meteen te glunderen... Maar: "mijn ei is gelegd" en of het ei van
Alissa ook is uitgebroed hoor je na de vakantie."
Frank Tinkelenberg:"Hier is mijn
oplossing voor de sudokupuzzel! Als beknopte oplossingshandleiding geef ik de
volgorde waarin ik de cijfers gevonden heb; hoe ik het allemaal precies gedaan
heb blijft gehuld in duisternis :)
f1, g1; a6, b4, b5; b7; b1, b3; a2; c1, d6, d8 (hint: a+b+c=108); a1; d7, d5;
h7; h6; e8; e7, f6; g6, c6; f7; d4; d3, a3, a4; d2, d1, e1; f2, e2, e3; g2, h2
en de rest is nu makkelijk :)"
Gabriele Carelli:"Here is the
solution for the pentomino-sudoku competition. At the beginning it seems a quite
hard competition but, looking further, it is a very, very hard ones! For the
solution I started considering the Y pentomino filling the b7 square, I
continued with the N pentomino (all squares), the I pentominoes (b1), then b3,
a2 and so on....
Thanks very much for this very interesting, and funning, sudoku variation (or
latin square variation?)"
Helmut Postl:"My sudoku explanation
is finish. Here it is. Have fun!
I’m still working on the other
pento problems."
Jan Kok:"Zeer bedankt voor de opgave, een
puzzel van deze soort zal me wel lukken hoop ik. Ik heb vakantie en met de buien
van deze dagen kom ik wel aan puzzelen (en lezen) toe.
Het oplossen was me een waar genoegen."
Juha Saukkola:"Solution started from
28525-pento left and most important thing was X-pento!
Nice problem!"
Klaus Rubrecht:"Op uw site ben ik voor de
eerste maal een pento-sudoku tegengekomen. Geprikkeld door de uitdaging ben ik
aan de slag gegaan.Trots op mijn oplossing wil ik natuurlijk aan de wedstrijd
deelnemen en zou ik graag kans maken op de TI-84, ik ben immers 17. Ook wil ik
eens één van die pygramsudoku's proberen en ik zou graag eentje ontvangen.
Ik ben op jullie site terechtgekomen via
www.wiskundemeisjes.nl bij de commentaren stond
er een link naar jullie mooie site. Ik heb net mijn school afgemaakt, ik zat in
het
Sint-Janscollege in Poperinge en volgde daar de
richting wiskunde-wetenschappen. Ik heb al eens mijn ogen laten vallen op de
moeilijke puzzel voor eeuwige roem, maar die
ziet er wel heel moeilijk uit. Niettemin zal ik toch eens proberen. Eerst zonder
de hint, misschien later met de hint. Hopelijk wordt het wat ... "
Michael Endick:"Rather than just give
the answer, I have created an animated GIF showing all the steps to solve it.
See the attachment. If you don't see the animation, try viewing it in Internet
Explorer or Firefox. Enjoy!"
Niels Wensink:"Was leuk om op te lossen!"
Peter Jeuken:"Het is me alleen gelukt de
locaties b7, a6, b5 en b4 te beredeneren. De rest heb ik met de computer
gevonden."
Ton Tillemans en Esther Pluess:"Vaak is de
tijd het probleem zoveel andere dingen te doen maar deze keer hebben we op onze
vakantiereis wat tijd genomen om een geslaagde beredenering te vinden"
Virginie Derycke:"Het grootste deel van de
sudoku heb ik zelf opgelost, maar soms vond ik he niet meer en dan heeft mijn
vader mij een beetje geholpen."
Bij vaststelling van fouten of onvolledigheid, mail
naar: