Wiskundeclub 101 - Luc Gheysens - Eekhout Academy 2025

Deze kanjers waren te vroeg en begonnen reeds te zoeken.

4V op een vierkant 5x5

Het op te vullen gebied van de haas moet een symmetrie-as hebben

In het laatste deel van de lessenreeks kwam het zwaartepunt aan bod.

Praktische methode om het zwaartepunt te bepalen.

Daar zijn ze: de pentomino's Let op onze reclame voor FlatPoly van Aad van de Wetering

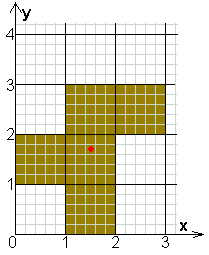
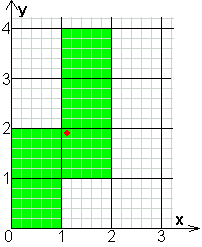
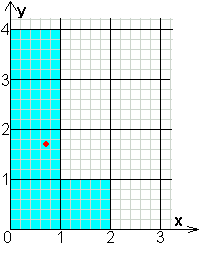
coördinaat van de middelpunten van de vijf vierkanten: (1,5;0,5) (1,5;1,5) (1,5;2,5) (0,5;1,5) (2,5;2,5) coördinaat van het zwaartepunt van F is (1,5;1,7)	coördinaat van de middelpunten van de vijf vierkanten: (0,5;0,5) (0,5;1,5) (0,5;2,5) (0,5;3,5) (1,5;0,5) coördinaat van het zwaartepunt van L is (0,7;1,7)	coördinaat van de middelpunten van de vijf vierkanten: (0,5;0,5) (0,5;1,5) (1,5;1,5) (1,5;2,5) (1,5;3,5) coördinaat van het zwaartepunt van N is (1,1;1,9)
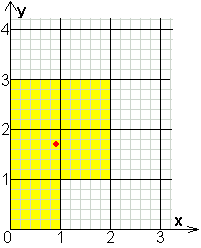
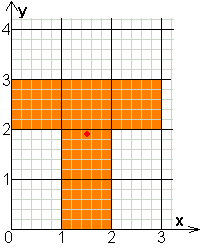
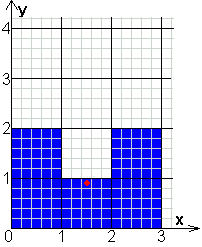
coördinaat van de middelpunten van de vijf vierkanten: (0,5;0,5) (0,5;1,5) (0,5;2,5) (1,5;1,5) (1,5;2,5) coördinaat van het zwaartepunt van P is (0,9;1,7)	coördinaat van de middelpunten van de vijf vierkanten: (0,5;2,5) (1,5;0,5) (1,5;1,5) (1,5;2,5) (2,5;2,5) coördinaat van het zwaartepunt van T is (1,5;1,9) Punt van de symmetrieas	coördinaat van de middelpunten van de vijf vierkanten: (0,5;0,5) (0,5;1,5) (1,5;0,5) (2,5;0,5) (2,5;1,5) coördinaat van het zwaartepunt van U is (1,5;0,9) Punt van de symmetrieas
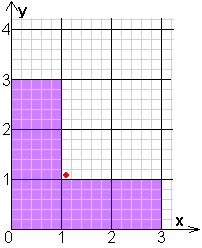
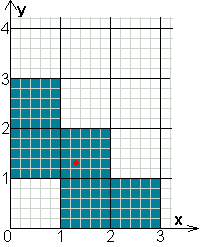
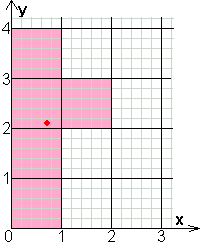
coördinaat van de middelpunten van de vijf vierkanten: (0,5;0,5) (0,5;1,5) (0,5;2,5) (1,5;0,5) (2,5;0,5) coördinaat van het zwaartepunt van V is (1,1;1,1) Punt van de symmetrieas.	coördinaat van de middelpunten van de vijf vierkanten: (0,5;1,5) (0,5;2,5) (1,5;0,5) (1,5;1,5) (2,5;0,5) coördinaat van het zwaartepunt van W is (1,3;1,3) Punt van de symmetrieas.	coördinaat van de middelpunten van de vijf vierkanten: (0,5;0,5) (0,5;1,5) (0,5;2,5) (0,5;3,5) (1,5;2,5) coördinaat van het zwaartepunt van Y is (0,7;2,1)

Het zwaartepunt van een vlakke figuur ligt op elke symmetrieas van die figuur. Als een vlakke figuur dus twee (of meer) symmetrieassen heeft, is het zwaartepunt precies het snijpunt van die symmetrieassen.
(I- en X-pentomino)
Als een vlakke figuur een symmetriemiddelpunt heeft dan is dat het zwaartepunt. (Z-pentomino)

Dan kwam een pentomino-spelletje
Kan je het vierkant (zonder het zwarte vierkant in het midden) volledig opvullen met de 12 verschillende pentomino's?

Je kan bewijzen dat dit het enige oppervlak is, dat het verschil is van 2 vierkanten, dat opvulbaar is met een pentominoset.
x² - y² = 60
Er zijn 65 oplossingen. Maar ze kregen een tip. Dan zijn er nog 6 oplossingen.
En ze vonden het!
 

Dit jaar bestaat de KULAK 60 jaar.
Ze vulden de cijfers 6 en 0 op met een pentominoset. Met FlatPoly wordt het opvullen van "60" een fluitje van een cent.