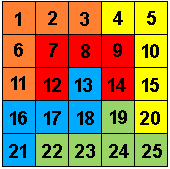
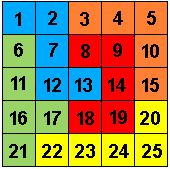
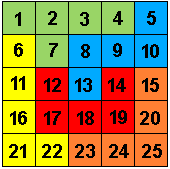
Omdat Matthijs Coster, Paul Levrie en Helmut Postl "60" worden in het jaar dat we deze pagina maken, dragen we de pagina aan hen op.
|
|
|
|
Naar aanleiding van de
potpourriproblemen 74 en
75
mailde Aad: "Hoe zijn de resultaten
bij een andere vierkantgrootte? "
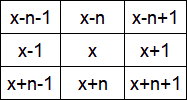
We gingen dus op zoek naar andere velden.
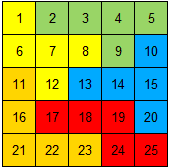
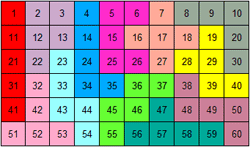
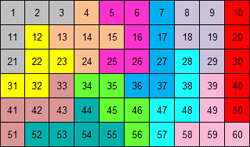
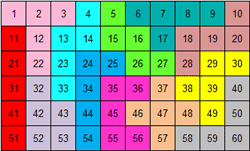
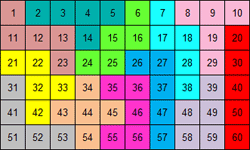
We kozen dus één van de
107
pentominovierkanten
van 5x5. Aangezien we getallen in de vakjes
plaatsen vervalt de symmetrie en zijn er 856 verschillende opgaven.
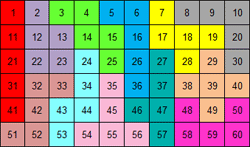
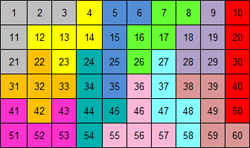
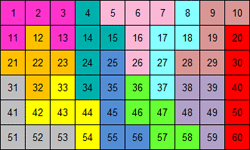
We gaven de voorkeur aan vierkanten zonder I- en P-pentomino en dan zijn er
nog 7 verschillende oplossingen.

Maak met de getallen in elke pentomino "60" door op te tellen, af te trekken, te
vermenigvuldigen of te delen. Je mag haakjes gebruiken.
We maakten van deze opgave een spel met twee personen.
Er is een spelbord, tweemaal de vijf pentomino's van het speelbord (in twee
verschillende kleuren) en een pentominodobbelsteen.

Iedere speler kiest een kleur pentomino's. De speler met de rode pentomino's
mag beginnen. Speler 1 gooit met de dobbelsteen. Hij probeert met de getallen in
de gegooide pentomino "60" te maken
door op te tellen, af te trekken, te vermenigvuldigen of te delen. Gooit men
het getal "60" op de dobbelsteen dan mag men de pentomino zelf kiezen.Heeft
men 60 dan legt men zijn eigen pentomino op het speelbord. Deze bedekt de
getallen waarmee men gerekend heeft. Heeft men geen 60 gevonden binnen een
bepaalde tijd dan mag de andere speler een mogelijke berekening geven om 60
te bekomen en met zijn pentomino de velden bedekken. Heeft geen van beiden
60 kunnen vinden dan legt degene die een resultaat gevonden heeft dichtst
bij 60 zijn pentomino op het bord leggen. Dan gaat de beurt naar speler 2.
Wie als eerste drie pentomino's op het bord gelegd heeft wint het spel.
We maakten een leukere uitvoering
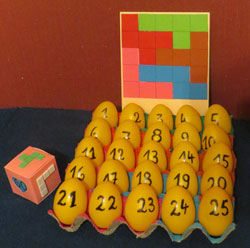
We hebben op het bord genummerde eitjes geplaatst. Het spel verloopt op
dezelfde manier maar als men wint legt men geen pentomino op het speelbord
maar neemt men de eitjes met de getallen erop waarmee men de "60" berekend
heeft. Wie 15 eitjes verzameld heeft, wint het spel.
Wil je voor deze borden voor elke pentomino een oplossing zien druk dan
hieronder.
![]()
Voor het eren van hun zestigste jaar zou de keuze van een 60-veld nog leuker
zijn.
Er zijn 2339
pentominorechthoeken
van 10x6.
Er is maar 1 oplossing waarbij we 2 rechthoeken van 5x6 kunnen leggen met
een set pentomino's.
We kozen één van de samenvoegingen van deze 2 rechthoeken voor ons 60-veld.

Maak met de getallen in elke pentomino "60" door op te tellen, af te trekken, te
vermenigvuldigen of te delen. Je mag haakjes gebruiken.
I: (31 x 41 - 11 x 1) : 21
Y: (13 + 4 - 2 - 3) x 5 of 2 x (3 x 4 + 5 + 13)
V: 6 x 7 + 26 + 8 - 16
N: 10 x (17 + 18 + 19) : 9
Z: 22 : (34 - 23) x 24 + 12
L: 14 x (25 - 15) - 35 - 45
X: 27 + 37 - 36 : (47 - 38)
F: (39 + 20 - 29 - 28) x 30
T: 42 - 32 + 51 + 52 - 53
W: 43 + 44 x 54 : 33 - 55
U: (48 - 46) x (57 - 56) + 58
P: 40 + 59 + 60 - 49 - 50
We zochten naar nog speciale "60 velden"
We kozen voor de twee rechthoeken van 10x6 die als enige een eigenschap
bezitten. Doordat de symmetrie vervalt omwille van de getallen hebben we 8
rechthoeken die de eigenschap bezitten. Weet je dewelke?
In de onderstaande gevallen is er geen enkele waar we met de getallen uit
elke pentomino 60 kunnen maken alleen met +, -, x, : en haken.
|
|
|
|
|
|
|
|
|
|
We kozen een willekeurige uit de
voorgaande acht.
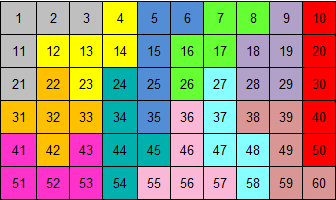
Maak met de getallen in elke pentomino "60" door op te tellen, af te trekken, te
vermenigvuldigen, te delen, tot een macht te verheffen of de wortel te
trekken. Je mag haakjes gebruiken.
Oplossing
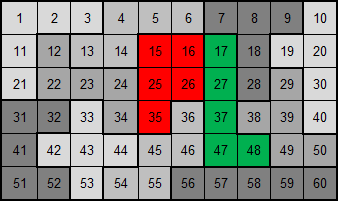
Omdat Paul Levrie gezegend is met initialen die pentominoletters
zijn kozen we voor dit pentomino-zestigveld. Het is de enige
pentominorechthoek waarbij de P en L niet langs de rand liggen.
De pentomino's bedekken telkens 5 getallen. Maak met deze getallen "60"
door op te tellen, af te trekken, te vermenigvuldigen, te delen, tot een
macht te verheffen, de vierkantwortel te trekken of faculteit te nemen. Je
mag haakjes plaatsen.
Oplossing
Voor Helmut maakten we er eentje op een 11x10 gevuld met de
pentomino's en tetromino's en voor Postl
voegden we nog een P-pentomino toe.

We kozen er eentje
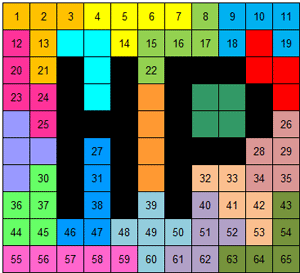
De pentomino's bedekken telkens 5 getallen. Maak met deze
getallen "60" door op te tellen, af te trekken, te vermenigvuldigen
en te delen.Je mag haakjes gebruiken.
Omwille van de getallen in de W-pentomino is ook de worteltrekking en de
faculteit toegelaten.
Oplossing
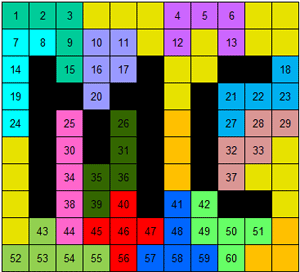
Voor Matthijs kozen we een rechthoek van 11x10 en vulden
die met een de pentomino's, tetromino's en tromino's.We plaatsten getallen
in de pentomino's.
Maak met de getallen van elke pentomino "60" door op te tellen, af te
trekken, te vermenigvuldigen en te delen.Je mag haakjes gebruiken.
Omwille van de getallen in de F-pentomino is ook de worteltrekking
toegelaten.
Oplossing
We zochten er eentje waar we de worteltrekking niet nodig hadden. We hebben
echter voor de tweede I-pentomino plakken nodig.
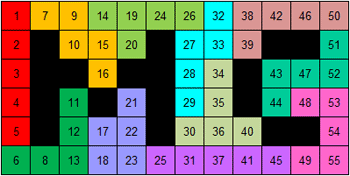
De pentomino's bevatten telkens 5 getallen. Maak met deze getallen 60 door
op te tellen, af te trekken, te vermenigvuldigen, te delen en te plakken. Je
mag haakjes plaatsen.
Oplossing
Extra opgaven zijn welkom.
We maakten er eentje voor Aad Thoen


Maak met de getallen in elke pentomino "67" door op te tellen, af te trekken, te
vermenigvuldigen of te delen. Je mag haakjes gebruiken.
Oplossing:
F: 1 + 6 x (7 + 12 - 8) = 67
Y: 2 x (3 x 9 + 4) + 5 = 67
T: 10 + 14 x (20 - 15) - 13 = 67
V: (11 + 16 - 23) x 22 - 21 = 67
N: 17 + 19 + 24 + 25 - 18 = 67
Op 16 november maakten we er eentje voor Aad van de Wetering


Maak met de getallen in elke pentomino "75" door op te tellen, af te trekken, te
vermenigvuldigen, te delen of tot de macht te verheffen. Je mag haakjes gebruiken.
Oplossing:
F: 1 + 6 + 7 x 8 + 12 = 75
Y: (2 x 3 x 4 - 9) x 5 = 75
T: 13 x 15 - 10 x 14 + 20 = 75
V: (23 - 21)^(22 - 16) + 11 = 75
N: (25 + 17) x 24 : 18 + 19 = 75
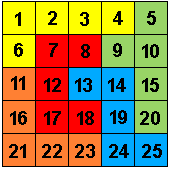
Omdat op de nationale wiskunde dagen 2020 Marjolein Kool
onze zaalvoorzitter is, maakten we voor haar een "62"-pentominospel.

We maakten een bord en nummerden 25 chocolaadjes.

Met hetzelfde speelbord kan men 4 verschillende spelen maken. (draaien van
het speelbord over 90°
|
|
|
|
|
Omdat men de 'milieuaspecten' heel belangrijk vindt, krijgen we maar een opgaveboekje per groepje en zijn er geen oplossingenboekjes.
Hieronder kan je allles downloaden
Opgaven op NWD
Oplossingen PQRS-Q 6
![]()
![]()