Jaarlijks maken we in het derde jaar in KSO Glorieux te Ronse een werk over de stelling van Pythagoras.
Lena en Ellen bekeken de stelling in 3D.

Ze zorgden er voor dat de som van de inhouden van de balken op de rechthoekszijden gelijk is aan de inhoud van de kubus op de schuine zijde. Op alle zijvlakken van de balken zijn prachtige toepassingen uitgewerkt. Heel wat pentomino’s zijn versneden tot vierkant.
De kubus op de schuine zijde (onderaan op de foto) is bedekt met een pentominoset.
Een pentominoset heeft een totale oppervlakte van 12x5=60. Een kubus heeft 6 zijvlakken dus moeten we een vierkant maken met oppervlakte 10. We kunnen 10 schrijven als de som van de kwadraten van 1 en 3. Dus als we een rechthoekige driehoek hebben met rechthoekszijden 1 en 3 dan is de schuine zijde ook de zijde van een vierkant met oppervlakte 10.
Zie ook het versnijden van 2 pentomino's tot een vierkant
Er was echter nog meer rekenwerk.
De kubus heeft een ribbe van 15 cm. De lengte van de zijde van een eenheidsvierkantje moet berekend worden.
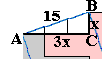
x² + (3x)² =15²
10x² = 225
x² = 22,5
De bedekking vonden ze op http://www.tzingaro.com/artelectric/pentominoes06.html
Andere sites waar je het beplakken van een kubus kan vinden:
http://home.planet.nl/~avdw3b/kubuspoly.html
http://home.educities.edu.tw/proteon/note131.htm
http://www.geocities.com/liviozuc/pag3_eng.html
http://www.ericharshbarger.org/pentominoes/article_06.html
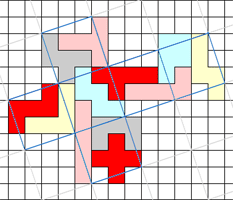
Je kan ook 2 kubussen bedekken met 1 set. Op elke kubus liggen dan 6
pentomino's. Dit betekent 1 pentomino op een zijvlak.
Zie het versnijden van
één pentomino tot een vierkant.
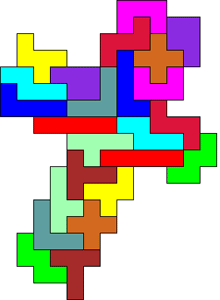
Hieronder zie je 4 mogelijke oplossingen.
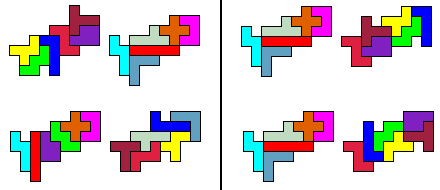
Een andere mogelijkheid is 2 sets gebruiken voor de bedekking van één kubus.
Op een zijvlak moet dan bedekt worden met een oppervlakte van 20.
Zie het versnijden van
vier pentomino's tot een vierkant.
Hieronder zie je een oplossing.
Opmerkingen?
Mail naar
o.d.m@fulladsl.be